Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-12T23:25:27.945Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Dihedral Main Conjectures of Iwasawa Theory for Hilbert Modular Eigenforms

Published online by Cambridge University Press:  20 November 2018

Jeanine Van Order
Jeanine Van Order*
Affiliation:
Section de Mathématiques, Ecole Polytechnique Fédérale de Lausanne, Lausanne 1015, Switzerland, e-mail: jeanine.vanorder@epfl.ch
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We construct a bipartite Euler system in the sense of Howard for Hilbert modular eigenforms of parallel weight two over totally real fields, generalizing works of Bertolini–Darmon, Longo, Nekovar, Pollack–Weston, and others. The construction has direct applications to Iwasawa's main conjectures. For instance, it implies in many cases one divisibility of the associated dihedral or anticyclotomic main conjecture, at the same time reducing the other divisibility to a certain nonvanishing criterion for the associated 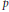$p$-adic 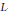$L$-functions. It also has applications to cyclotomic main conjectures for Hilbert modular forms over 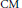$\text{CM}$ fields via the technique of Skinner and Urban.

Keywords

11G1011G1811G40Iwasawa theoryHilbert modular formsabelian varieties
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 65 , Issue 2 , 01 April 2013 , pp. 403 - 466
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Bertolini, M. and Darmon, H., Derived heights and generalized Mazur-Tate regulators. Duke Math. J. 76(1994), no. 1, 75–111. http://dx.doi.org/10.1215/S0012-7094-94-07604-7 Google Scholar
[2] Bertolini, M., Heegner points on Mumford-Tate curves. Invent. Math. 126(1996), no. 3, 413–456. http://dx.doi.org/10.1007/s002220050105 Google Scholar
[3] Bertolini, M., Iwasawa's main conjecture for elliptic curves over anticyclotomic Zp-extensions. Ann. of Math. 162(2005), no. 1, 1–64. http://dx.doi.org/10.4007/annals.2005.162.1 Google Scholar
[4] Bertolini, M., A rigid-analytic Gross-Zagier formula and arithmetic applications. Invent. Math. 126(1996), no. 3, 413–456. http://dx.doi.org/10.1007/s002220050105 Google Scholar
[5] Bosch, S.,Lütkebohmert, W., and Raynaud, M., Néron models. Ergebnisse der Mathematik und Ihre Grenzgebiete (3), 21, Springer- Verlag, Berlin, 1990.Google Scholar
[6] Bourbaki, N., Élements de mathématique, Fasc. XXXI, Algèbre commutative, Chapitre 7: Diviseurs. Actualiés Scientifiques et Industrielles, 1314, Paris, Hermann, 1965.Google Scholar
[7] Boutot, J.-F. and Carayol, H. Uniformisation p-adique des courbes de Shimura: les thèoreèmes de Cerednik et Drinfeld. Courbes modulaires et courbes de Shimura (Orsay, 1987/1988). Astérisque 196-197(1991), 7, 45–158.Google Scholar
[8] Buzzard, K., Integral models of certain Shimura curves. Duke Math. J. 87(1997), no. 3, 591–612. http://dx.doi.org/10.1215/S0012-7094-97-08719-6 Google Scholar
[9] Carayol, H., Sur la mauvaise réduction des courbes de Shimura. Compositio Math. 59(1986), no. 2, 151–230.Google Scholar
[10] Carayol, H., Sur les représentations galoisiennes modulo l attachées aux formes modulaires. Duke. Math J.. 59(1989), no. 3, 785–801. http://dx.doi.org/10.1215/S0012-7094-89-05937-1 Google Scholar
[11] Cerednik, I. V., Uniformization of algebraic curves by discrete arithmetic subgroups of PGL2(kw) with compact quotient spaces. (Russian) Math. Sb. 100(142)(1976) no. 1, 59–88; translated in Math. USSR Sbornik, 29(1976), 55-78.Google Scholar
[12] Cheng, C., Multiplicities of Galois representations in cohomology groups of Shimura curves over totally real field. Ph.D. thesis, Northwestern University, 2011.Google Scholar
[13] Cheng, C., Ihara's lemma for Shimura curves. preprint, 2011.Google Scholar
[14] Coates, J. and Greenberg, R., Kummer theory for abelian varieties over local fields. Invent. Math. 124(1996), no. 1-3, 129–174. http://dx.doi.org/10.1007/s002220050048 Google Scholar
[15] Cornut, C. and Vatsal, V., CM points and quaternion algebras. Doc. Math. 10(2005), 263–309.Google Scholar
[16] Cornut, C., Nontriviality of Rankin-Selberg L-functions and CM points. In: L-functions and Galois representations, London Math. Soc. Lecture Note Ser., 320, Cambridge University Press, Cambridge, 2007, pp. 121–186.Google Scholar
[17] Diamond, F., The Taylor-Wiles construction and multiplicity one. Invent. Math. 128(1997), no. 2, 379–391. http://dx.doi.org/10.1007/s002220050144 Google Scholar
[18] Diamond, F. and Taylor, R., Nonoptimal levels of mod l modular representations. Invent. Math. 115(1994), no. 3, 435–462. http://dx.doi.org/10.1007/BF01231768 Google Scholar
[19] Dimitrov, M., Galois representations modulo p and cohomolgy of Hilbert modular varieties. Ann. Sci. É cole Norm. Sup. (4) 38(2005), no. 4, 505–551.Google Scholar
[20] Drinfeld, V., Coverings of p-adic symmetric domains. (Russian), Funkcional. Anal. i Prilozen. 10(1976), no. 2, 29-40; translated in Funct. Anal. Appl. 10(1976), 107–115.Google Scholar
[21] Drinfeld, V., Elliptic modules. (Russian) Mat. Sb. (N.S.) 94(136)(1974), 594–627, 656.Google Scholar
[22] B. Edixhoven, Appendix in [4].Google Scholar
[23] Fouquet, O., Dihedral Iwasawa theory of nearly ordinary quaternionic automorphic forms. 2009, http://www.math.u-psud.fr/_fouquet/src/DihedralFouquet.pdf.Google Scholar
[24] Garrett, P. B., Holomorphic Hilbert modular forms. The Wadsworth & Brooks/Cole Mathematics Series.Wadsworth & Brooks/Cole Advanced Books & Software, Pacific Grove, CA, 1990.Google Scholar
[25] van der Geer, G., Hilbert modular surfaces. Ergebnisse der Mathematik und ihrer Grenzgebiete (3), 16, Springer-Verlag, Berlin, 1988.Google Scholar
[26] Goren, E. Z., Lectures on Hilbert modular varieties and modular forms. CRM Monograph Series, 14 American Mathematical Society, Providence, RI, 2001.Google Scholar
[27] Grothendieck, A., ed., Groupes de monodromie en géométrie algébrique, Séminaire de Géometrie Algébrique du Bois-Marie 1967–1969. Lecture Notes in Math., 228, Springer-Verlag, Berlin-New York, 1972.Google Scholar
[28] Hachimori, Y. and Venjakob, O., Completely faithful Selmer groups over Kummer extensions. Doc. Math. 2003, Extra Vol., 443–478.Google Scholar
[29] Howard, B., Bipartite Euler systems. J. Reine Angew. Math. 597(2006), 1–25. http://dx.doi.org/10.1515/CRELLE.2006.062 Google Scholar
[30] Howard, B., Iwasawa theory of Heegner points on abelian varieties of GL2-type. Duke Math. J. 124(2004), no. 1, 1–45. http://dx.doi.org/10.1215/S0012-7094-04-12411-X Google Scholar
[31] Ihara, Y., Shimura curves over finite fields and their rational points. In: Applications of curves over finite fields (Seattle,WA, 1997), Contemp. Math., 245, American Mathematical Society, Providence, RI, 1999, pp. 15–23.Google Scholar
[32] Jacquet, H. and Langlands, R. P., Automorphic forms on GL(2). Lecture Notes in Mathematics, 114, Springer-Verlag, Berlin-New York, 1970.Google Scholar
[33] Jarvis, F., Mazur's principle for totally real fields. Compositio Math. 116(1999), no. 1, 39–79. http://dx.doi.org/10.1023/A:1000600311268 Google Scholar
[34] Jarvis, F., Level lowering for modular mod l representations over totally real fields. Math. Ann. 313(1999), no. 1, 141–160. http://dx.doi.org/10.1007/s002080050255 Google Scholar
[35] Jordan, B.W. and Livné, R. A., Local Diophantine properties of Shimura curves. Math. Ann. 270(1985), no. 2, 235–248. http://dx.doi.org/10.1007/BF01456184 Google Scholar
[36] Kato, K., p-adic Hodge theory and values of zeta functions of modular forms. Cohomologies p-adiques et applications arithmétiques. III. Astérisque 295(2004), ix, 117–290.Google Scholar
[37] Katz, N. M. and Mazur, B., Arithmetic moduli of elliptic curves. Annals of Mathematics Studies, 108, Princeton University Press, Princeton, NJ, 1985.Google Scholar
[38] Kisin, M., Moduli of finite flat group schemes, and modularity. Ann. of Math. 170(2009), no. 3, 1085–1180. http://dx.doi.org/10.4007/annals.2009.170.1085 Google Scholar
[39] Kurihara, A., On some examples of equations defining Shimura curves and the Mumford uniformization. J. Fac. Sci. Univ. Tokyo Sect. IA Math. 25(1979), no. 3,277–300.Google Scholar
[40] Ling, S., Shimura subgroups of Jacobians of Shimura curves. Proc. Amer. Math. Soc. 118(1993), no. 2, 385–390. http://dx.doi.org/10.1090/S0002-9939-1993-1145947-2 Google Scholar
[41] Longo, M., Anticyclotomic Iwasawa's main conjecture for Hilbert modular forms. Commentarii Mathematici Helvetici, to appear.Google Scholar
[42] Longo, M., Euler systems obtained from congruences between Hilbert modular forms. Rend. Semin. Mat. Univ. Padova 18(2007), 1–34.Google Scholar
[43] Longo, M., On the Birch and Swinnerton-Dyer conjecture for modular elliptic curves over totally real fields. Ann. Inst. Fourier (Grenoble) 56(2006), no. 3, 689–733. http://dx.doi.org/10.5802/aif.2197 Google Scholar
[44] Mazur, B. and Rubin, K., Kolyvagin systems. Mem. Amer. Math. Soc. 168(2004), no. 799.Google Scholar
[45] Mazur, B. and Wiles, A., Class fields of abelian extensions of Q. Invent. Math. 76(1984), no. 2, 179–330. http://dx.doi.org/10.1007/BF01388599 Google Scholar
[46] Milne, J. S., Arithmetic duality theorems. Perspectives in Mathematics, 1. Academic Press, Boston, MA, 1986.Google Scholar
[47] Morita, Y., Reduction modulo p of Shimura curves. Hokkaido Math. J. 10(1981), no. 2, 209–238.Google Scholar
[48] Mumford, D., An analytic construction of degenerating curves over complete local rings Compos. Math. 24(1972), 129–174.Google Scholar
[49] Nekovar, J., Level raising and anticyclotomic Selmer groups for Hilbert modular forms of weight two. Canad. J. Math., to appear. http://dx.doi.org/10.4153/CJM-2011-077-6.Google Scholar
[50] Pollack, R. and Weston, T., On anticyclotomic μ-invariants of modular forms. Compositio Math., to appear. http://dx.doi.org/10.1112/S0010437X11005318 Google Scholar
[51] Rajaei, A., On the levels of mod l Hilbert modular forms. J. Reine Angew. Math. 537(2001), 33–65. http://dx.doi.org/10.1515/crll.2001.058 Google Scholar
[52] Raynaud, M., Spécialization du foncteur de Picard. Inst. Hautes Études Sci. Publ. Math. 38(1970), 27–76.Google Scholar
[53] Ribet, K., Bimodules and abelian surfaces. In: Algebraic number theory, Adv. Stud. Pure. Math., 17, Academic Press, Boston, MA, 1989, pp. 359–407.Google Scholar
[54] Ribet, K., On modular representations of Gal(Q/Q) arising from modular forms. Invent. Math. 100(1990), no. 2, 431–476. http://dx.doi.org/10.1007/BF01231195 Google Scholar
[55] Serre, J.-P., Propriétés galoisiennes des points d’ordre fini des courbes elliptiques. Invent. Math. 15(1972), no. 4, 259–331. http://dx.doi.org/10.1007/BF01405086 Google Scholar
[56] Shimura, G., The special values of zeta functions associated with Hilbert modular forms. Duke Math. J. 45(1978), no. 3, 637–679. http://dx.doi.org/10.1215/S0012-7094-78-04529-5 Google Scholar
[57] Skinner, C. and Urban, E., The Iwasawa main conjectures for GL2. http://www.math.columbia.edu/_urban/eurp/MC.pdf.Google Scholar
[58] Tate, J. T., Global class field theory. In: Algebraic Number Theory (Proc. Instructional Conf., Brighton, 1965), Thompson, Washington, D.C., 1967, pp. 162–203.Google Scholar
[59] Tate, J. T., Relations between K2 and Galois cohomology. Invent Math. 36(1976), 257–274. http://dx.doi.org/10.1007/BF01390012 Google Scholar
[60] Taylor, R., On Galois representations associated to Hilbert modular forms. Invent. Math. 98(1989), no. 2, 265–280. http://dx.doi.org/10.1007/BF01388853 Google Scholar
[61] Van Order, J., On the dihedral Euler characteristics of Selmer groups of abelian varieties. arxiv:abs/1112.3825 Google Scholar
[62] Van Order, J., On the quaternionic p-adic L-functions associated to Hilbert modular eigenforms. arxiv:abs/1112.3821.Google Scholar
[63] Vatsal, V., Special values of anticyclotomic L-functions. Duke Math. J. 116(2003), no. 2, 219–261. http://dx.doi.org/10.1215/S0012-7094-03-11622-1 Google Scholar
[64] Varshavsky, Y., P-adic uniformization of unitary Shimura varieties. Inst. Hautes Études Publ. Math. 87(1998), 57–119.Google Scholar
[65] Varshavsky, Y., P-adic uniformization of unitary Shimura varieties. II. J. Differential Geom. 49(1998), no. 1, 75–113.Google Scholar
[66] Vignéras, M.-F., Arithmétique des algèbres des quaternions. Lecture Notes in Mathematics, 800, Springer, Berlin, 1980.Google Scholar
[67] Waldspurger, J.-P., Sur les valeurs de certaines fonctions L automorphes en leur centre de symétrie. Compositio Math. 54(1985), no. 2, 173–242.Google Scholar
[68] Wan, X., Ph.D. Thesis, Princeton University, in progress.Google Scholar
[69] Wan, X., On ordinary λ-adic representations associated to modular forms. Invent. Math. 94(1988), no. 3, 529–573. http://dx.doi.org/10.1007/BF01394275 Google Scholar
[70] Yuan, X., Zhang, S.-W., and W.|Zhang, Heights of CM points I: Gross-Zagier formula. http://www.math.columbia.edu/_szhang/papers/HCMI.pdf.Google Scholar
[71] Zhang, S.-W., Gross-Zagier formular for GL2. Asian J. Math. 5(2001), no. 2, 183–290.Google Scholar
[72] Zhang, S.-W., Heights of Heegner points on Shimura curves. Ann. of Math. 153(2001), no. 1, 27–147. http://dx.doi.org/10.2307/2661372 Google Scholar