Hostname: page-component-848d4c4894-m9kch Total loading time: 0 Render date: 2024-06-08T18:34:07.883Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Hasse-Minkowski Invariant of the Kronecker Product of Matrices

Published online by Cambridge University Press:  20 November 2018

Manohar N. Vartak
Manohar N. Vartak*
Affiliation:
University of Bombay, India
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let R = (rij) be an m × n matrix and let S = (sik) be dip × q matrix denned over a field F. The Kronecker product R × S of R and S is denned as follows:

Definition 1.1. The Kronecker product R × S of the matrices R and S is given by 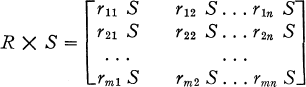where rij S; i = 1, 2, … , m; j = 1, 2, … , n, is itself a p × q matrix (1, 69-70).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 10 , 1958 , pp. 66 - 72
Copyright
Copyright © Canadian Mathematical Society 1958

References

1. Murnaghan, F. D., The Theory of Group Representation (Baltimore, 1938).Google Scholar
2.Jones, B. W., The Arithmetic Theory of Quadratic Forms (New York, 1950).Google Scholar
3. MacDuffee, C. C. Theory of Matrices (New York, 1946).Google Scholar
4. Bose, R. C. and Connor, W. S., Combinatorial properties of group-divisible incomplete block designs, Ann. Math. Stat., 23 (1952), 367-383.Google Scholar
5. Vartak, M. N., On an application of the Kronecker product of matrices to statistical designs, Ann. Math. Stat., 26 (1955), 420-438.Google Scholar