Hostname: page-component-848d4c4894-ttngx Total loading time: 0 Render date: 2024-06-01T21:57:10.245Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Radius of Curvature for Convex Analytic Functions

Published online by Cambridge University Press:  20 November 2018

Paul Eenigenburg
Paul Eenigenburg*
Affiliation:
Western Michigan University, Kalamazoo, Michigan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Definition 1.1. Let 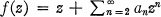be analytic for |z| < 1. If ƒ is univalent, we say that ƒ belongs to the class S.

Definition 1.2. Let ƒ ∈ S, 0 ≦ α < 1. Then ƒ belongs to the class of convex functions of order α, denoted by Kα, provided

(1)

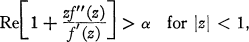
and if > 0 is given, there exists Z0, |Z0| < 1, such that

Let ƒ ∈ Kα and consider the Jordan curve ϒτ = ƒ(|z| = r), 0 < r < 1. Let s(r, θ) measure the arc length along ϒτ; and let ϕ(r, θ) measure the angle (in the anti-clockwise sense) that the tangent line to ϒτ at ƒ(reiθ) makes with the positive real axis.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 22 , Issue 3 , 01 June 1970 , pp. 486 - 491
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Hardy, G. H., Littlewood, J. E., and Polya, G., Inequalities (Cambridge, at the University Press, 1967).Google Scholar
2. Hayman, W. K., The asymptotic behaviour of p-valent functions, Proc. London Math. Soc. (3) 5 (1955), 257–284.Google Scholar
3. Hille, E., Analytic function theory, Vol. II (Blaisdell, New York, 1962).Google Scholar
4. Keogh, F. R., Some inequalities for convex and star-shaped domains, J. London Math. Soc. 29 (1954), 121–123.Google Scholar