Hostname: page-component-848d4c4894-x24gv Total loading time: 0 Render date: 2024-06-08T14:20:31.242Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Resolution Diagrams of the Brieskorn Singularities (2,q,r) of Type II

Published online by Cambridge University Press:  20 November 2018

Akio Yamada  and
Yukio Matsumoto
Akio Yamada
Affiliation:
University of Tokyo, Komaba, Tokyo
Yukio Matsumoto
Affiliation:
University of Tokyo, Hongo, Tokyo
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let p, q, r be pairwise coprime integers with 2 ≦ p < q < r. The equation 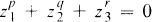defines a complex hypersurface V(p, q, r) ⊂ C3 which has an isolated singular point at the origin. We call the singularity the Brieskorn singularity (p, q, r). An algorithm of resolving this singularity is known [1]. According to the algorithm, the resolution diagram which describes the configuration of the pre-image of the singular point in the resolved surface is a star-shaped tree Γp, q, r with three branches:

1.1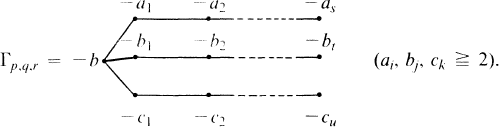

The positive integers (weights) ai, bj, ck are given as follows: Let x, y, z, b be integers satisfying

1.2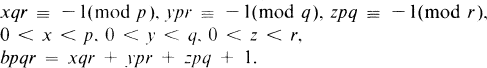

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 35 , Issue 6 , 01 December 1983 , pp. 1049 - 1058
Copyright
Copyright © Canadian Mathematical Society 1983

References

1. Hirzebruch, F., Neumann, W. D. and Koh, S. S., Differentiable manifolds and quadratic forms (Dekker, New York, 1971).Google Scholar
2. Milnor, J. and Husemoller, D., Symmetric bilinear forms (Springer, New York, 1973).CrossRefGoogle Scholar
3. Neumann, W. D., An invariant of plumbed homology spheres, in: Topology symposium Siegen 1979, Proceedings, Lecture notes in mathematics 788 (Springer, 1980), 125–144.Google Scholar
4. Neumann, W. D. and Raymond, F., Seifert manifolds, plumbing, [x-invariant and orientation reversing maps, in: Algebraic and geometric topology symposium Santa Barbara 1977, Proceedings, Lecture notes in mathematics 664 (Springer, 1978), 163–196.Google Scholar
5. Yamada, A. and Matsumoto, Y., Network induction and resolution diagrams of the Brieskorn singularities, to appear in Scientific Papers of the College of Arts and Sciences 33 (1983), University of Tokyo.Google Scholar