Article contents
On the Singularities of Plane Curves
Published online by Cambridge University Press: 20 November 2018
Extract
Let Γ be a differentiable curve in a real projective plane P2 met by every line of P2 at a finite number of points. The singular points of Γ are inflections, cusps (cusps of the first kind) and beaks (cusps of the second kind). Let n1(Γ), n2(Γ) and n3(Γ) be the number of these points in Γ respectively. Then Γ is non-singular if
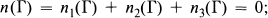
otherwise, Γ is singular.
We wish to determine when T is singular and then find the minimum value of n(Γ). A history and an analysis of this problem were presented in [1] and [2]. It was shown that we may assume that Γ is a curve of even order (even degree if Γ is algebraic), met by every line in P2. Then if Γ does not contain any multiple points or if Γ contains only a certain type of multiple point, Γ is singular. Presently, we complete this investigation
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1986
References
- 2
- Cited by


