Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T01:48:06.226Z Has data issue: false hasContentIssue false
  • English
  • Français

Pointwise Convergence of Alternating Sequences

Published online by Cambridge University Press:  20 November 2018

M. A. Akcoglu  and
L. Sucheston
M. A. Akcoglu
Affiliation:
University of Toronto, Toronto, Ontario
L. Sucheston
Affiliation:
The Ohio State University, Columbus, Ohio
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 1 < p < ∞ and let Lp be the usual Banach Space of complex valued functions on a σ-finite measure space. Let (Tn), n ≧ 1, be a sequence of positive linear contractions on Lp. Hence and 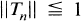, where 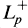is the part of Lp that consists of non-negative Lp functions. The adjoint of Tn is denoted by 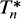which is a positive linear contraction of Lq with q = p/(p — 1).

Our purpose in this paper is to show that the alternating sequences associated with (Tn), as introduced in [2], converge almost everywhere. Complete definitions will be given later. When applied to a non negative function, however, this result is reduced to the following theorem.

(1.1) THEOREM. If (Tn) is a sequence of positive contractions of Lp then (1.2)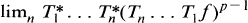

exists a.e. for all.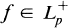

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 40 , Issue 3 , 01 June 1988 , pp. 610 - 632
Copyright
Copyright © Canadian Mathematical Society 1988

References

1. Akcoglu, M. A., A pointwise ergodic theorem in Lp-spaces, Can. J. Math. 26 (1975), 1075–1082.Google Scholar
2. Akcoglu, M. A. and Sucheston, L., An alternating procedure for operators on Lp-spaces, Proc. AMS, to appear.Google Scholar
3. Burkholder, D. L. and Chow, Y. S., Iterates of conditional expectation operators, Proc. AMS 12 (1961), 490–495.Google Scholar
4. Doob, J. L., A ratio operator limit theorem, Z. Wahrsch. 1 (1963), 288–294.Google Scholar
5. Krengel, U., Ergodic theorems, de Gruyter Studies in Math. 6 (1985).CrossRefGoogle Scholar
6. Mazur, S., Une remarque sur Vhoméomorphie des champs fonctionnels, Studia Math. 1 (1929), 83–85.Google Scholar
7. Rota, G. C., An “Alternierende Verfahren” for general positive operators, Bull. AMS. 68 (1962), 95–102.Google Scholar
8. Starr, N., Operator limit theorems, Trans. AMS 121 (1966), 90–115.Google Scholar
9. Stein, E., On the maximal ergodic theorem, Proc. Nat. Acad. Sci. USA, 47 (1961), 1894–1897.Google Scholar
10. Stein, E., Topics in harmonic analysis (Princeton Univ. Press, 1970).Google Scholar