Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Fliess, Michel
1973.
Propriétés booléennes des langages stochastiques.
Mathematical Systems Theory,
Vol. 7,
Issue. 4,
p.
353.
Phan Dinh Di�u
1977.
Criteria of representability of languages in probabilistic automata.
Cybernetics,
Vol. 13,
Issue. 3,
p.
352.

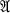 denote the set of functions of a complex variable
denote the set of functions of a complex variable