Hostname: page-component-848d4c4894-wg55d Total loading time: 0 Render date: 2024-06-09T03:57:18.496Z Has data issue: false hasContentIssue false
  • English
  • Français

Prehomogeneity on Quasi-Split Classical Groups and Poles of Intertwining Operators

Published online by Cambridge University Press:  20 November 2018

Xiaoxiang Yu
Xiaoxiang Yu*
Affiliation:
Department of Mathematics, Xuzhou Normal University, 29 Shanghai Road, Xuzhou, China, 221116, tianyuanwing@yahoo.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Suppose that 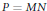$P=MN$ is a maximal parabolic subgroup of a quasisplit, connected, reductive classical group 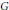$G$ defined over a non-Archimedean field and 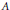$A$ is the standard intertwining operator attached to a tempered representation of 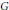$G$ induced from 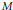$M$ . In this paper we determine all the cases in which Lie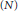$(N)$ is prehomogeneous under 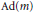$\text{Ad}\left( m \right)$ when 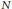$N$ is non-abelian, and give necessary and sufficient conditions for 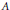$A$ to have a pole at $0$.

Keywords

22E5020G05
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 61 , Issue 3 , 01 June 2009 , pp. 691 - 707
Copyright
Copyright © Canadian Mathematical Society 2009

References

[1] Goldberg, D. and Shahidi, F., On the tempered spectrum of quasi-split classical groups. Duke Math. J. 92(1998), no. 2, 255–294.Google Scholar
[2] Goldberg, D. and Shahidi, F., On the tempered spectrum of quasi-split classical groups. II. Canad. J. Math. 53(2001), no. 2, 244–277.Google Scholar
[3] Harish-Chandra, , Harmonic Analysis on Real Reductive Groups, III. Ann of Math. 104 (1976), 117–201.Google Scholar
[4] Harish-Chandra, , Harmonic analysis on reductive p-adic groups. In: Proc. Sympos. Pure Math. 26, American Mathematical Society, Providence, RI, 1973, pp. 167–192.Google Scholar
[5] Humphreys, J., Introduction to Lie Algebras and representation theory. Second printing, revised, Graduate Texts in Mathematics 9, Springer-Verlag, New York-Berlin, 1978.Google Scholar
[6] Muller, I., Dècomposition orbitale des espaces prèhomogènes règuliers de type parabolique commutatif et application. C. R Acad. Sci. Paris Sèr. I Math. 303(1986), no. 11, 495–498.Google Scholar
[7] Sato, M. and Kimura, T., A classification of irreducible prehomogeneous vector space and their relative invariants. Nagoya Math. J. 65(1977), 1-155.Google Scholar
[8] Shahidi, F., A proof of Langlands’ conjecture on Plancherel measures; complementary series for p-adic groups. Ann of Math. 132(1990), no. 2, 273–330.Google Scholar
[9] Shahidi, F., Twisted endoscopy and reducibility of induced representation for p-adic groups. Duke Math. J. 66(1992), no. 1, 1–41.Google Scholar
[10] Shahidi, F., Poles of intertwining operators via endoscopy: the connection with prehomogeneous vector spaces. Compositio Math. 120(2000), no. 3, 291–325.Google Scholar
[11] Vinberg, È. B., TheWeyl group of a graded Lie algebra. Izv. Akad. Nauk SSSR Ser. Mat. 40(1976), no. 3, 488–526, 709. (1976), 463-495.Google Scholar
[12] Yu, X., Centralizer and twisted centralizers: application to intertwining operators. Canad. J. Math. 58(2006), no. 3, 643–672.Google Scholar
[13] Bernstein, I. N. and Zelevinskii, A. V., Representation of the group GL(n, F) where F is a local non-archimedean field. Russian Math. Surveys 31(1976), no. 3, 1–68.Google Scholar