No CrossRef data available.
Article contents
Pure Infiniteness of the Crossed Product of an AH-Algebra by an Endomorphism
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
It is shown that simplicity of the crossed product of a unital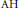 
$\text{AH}$-algebra with slow dimension growth by an endomorphism implies that the algebra is also purely infinite, provided only that the endomorphism leaves no trace state invariant and takes the unit to a full projection.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2012
References
[An]
Anantharaman-Delaroche, C., Purely infinite C*-algebras arising from dynamical systems.
Bull. Soc. Math. France
125(1997), no. 2, 199–225.Google Scholar
[BKR]
Boyd, S., Keswari, N., and Raeburn, I., Faithful representations of crossed products by endomorphisms.
Proc. Amer. Math. Soc.
118(1993), no. 2, 427–436. http://dx.doi.org/10.1090/S0002-9939-1993-1126190-X
Google Scholar
[CT]
Carlsen, T. M. and Thomsen, K., The structure of the C*-algebra of a locally injective surjection. Ergodic Theory and Dynamical Systems, to appear, available on CJO 2011. http://dx.doi.org/10.1017/S0143385711000216 http://dx.doi.org/10.1007/s00220-010-1168-7
Google Scholar
[De]
Deaconu, V., Groupoids associated with endomorphisms.
Trans. Amer. Math. Soc.
347(1995), no. 5, 1779–1786. http://dx.doi.org/10.2307/2154972
Google Scholar
[DR]
Dykema, K. and M. Rørdam, Purely infinite, simple C*-algebras arising from free product constructions.
Canad. J. Math.
50(1998), no. 2, 323–341. http://dx.doi.org/10.4153/CJM-1998-017-x
Google Scholar
[KR]
Kirchberg, E. and M. Rørdam, Non-simple purely infinite C*-algebras.
Amer. J. Math.
122(2000), no. 3, 637–666. http://dx.doi.org/10.1353/ajm.2000.0021
Google Scholar
[OP1]
Olesen, D. and Pedersen, G. K., Applications of the Connes spectrum to C*-dynamical systems.
J. Funct. Anal.
30(1978), no. 2, 179–197. http://dx.doi.org/10.1016/0022-1236(78)90069-1
Google Scholar
[OP2]
Olesen, D. and Pedersen, G. K., Applications of the Connes spectrum to C*-dynamical systems. III.
J. Funct. Anal.
45(1982), no. 3, 357–390. http://dx.doi.org/10.1016/0022-1236(82)90011-8
Google Scholar
[Pe]
Pedersen, G. K., C*-algebras and their automorphism groups.
London Mathematical Society Monographs, 14, Academic Press, London-New York, 1979.Google Scholar
[PS]
Putnam, I. and Spielberg, J., The structure of C*-algebras associated with hyperbolic dynamical systems.
J. Func. Anal.
163(1999), no. 2, 279–299. http://dx.doi.org/10.1006/jfan.1998.3379
Google Scholar
[R1]
Rørdam, M., Classification of certain infinite simple C*-algebras.
J. Funct. Anal.
131(1995), no. 2, 415–458. http://dx.doi.org/10.1006/jfan.1995.1095
Google Scholar
[R2]
Rørdam, M., Classification of certain infinite simple C*-algebras. III. In: Operator algebras and their applications (Waterloo, ON, 1994/1995), Fields Inst. Commun., 13, American Mathematical Society, 1997.Google Scholar
[St]
Stacey, P. J., Crossed products of C*-algebras by endomorphisms.
J. Austral. Math. Soc.
54(1993), no. 2, 204–212. http://dx.doi.org/10.1017/S1446788700037113
Google Scholar
[Th1]
Thomsen, K., Semi-étale groupoids and applications.
Ann. Inst. Fourier
60(2010), no. 3, 759–800. http://dx.doi.org/10.5802/aif.2539
Google Scholar
[Th2]
Thomsen, K., Inductive limits of interval algebras: the simple case. In: Quantum and non-commutative analysis (Kyoto, 1992), Math. Phys. Stud., 16, Kluwer Acad. Publ. Dordrecht, 1993, 399–404.Google Scholar
[T]
Toms, A. S., Comparison theory and smooth minimal C*-dynamics.
Comm. Math. Phys.
289(2009), no. 2, 401–433. http://dx.doi.org/10.1007/s00220-008-0665-4
Google Scholar
[W]
Winter, W., Nuclear dimension and Z-stability of perfect C*-algebras. arxiv:1006.2731v1Google Scholar
You have
Access