Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T20:17:14.592Z Has data issue: false hasContentIssue false
  • English
  • Français

Random Walks in Degenerate Random Environments

Published online by Cambridge University Press:  20 November 2018

Mark Holmes  and
Thomas S. Salisbury
Mark Holmes
Affiliation:
Department of Statistics, University of Auckland, Auckland, New Zealand. e-mail: mholmes@stat.auckland.ac.nz
Thomas S. Salisbury
Affiliation:
Department of Mathematics and Statistics, York University, Toronto, ON. e-mail: salt@yorku.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

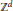We study the asymptotic behaviour of random walks in i.i.d. random environments on ${{\mathbb{Z}}^{d}}$. The environments need not be elliptic, so some steps may not be available to the random walker. We prove a monotonicity result for the velocity (when it exists) for any 2-valued environment, and show that this does not hold for 3-valued environments without additional assumptions. We give a proof of directional transience and the existence of positive speeds under strong but non-trivial conditions on the distribution of the environment. Our results include generalisations (to the non-elliptic setting) of 0-1 laws for directional transience and, in 2-dimensions, the existence of a deterministic limiting velocity.

Keywords

60K37Random walknon-elliptic random environmentzero-one lawcoupling
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 66 , Issue 5 , 01 October 2014 , pp. 1050 - 1077
Copyright
Copyright © Canadian Mathematical Society 2014

References

[1] Basdevant, A.-L. and Singh, A., On the speed of a cookie random walk. Probab. Theory Relat. Fields. 141(2008), no. 3–4, 625–645. http://dx.doi.org/10.1007/s00440-007-0096-8 Google Scholar
[2] Berger, N. and Deuschel, J.-D., A quenched invariance principle for non-elliptic random walk in i.i.d. balanced random environment. Probab. Theory Related Fields, to appear, 2013. http://dx.doi.org/10.1007/s00440-012-0478-4 Google Scholar
[3] Bolthausen, E., Sznitman, A.-S., and Zeitouni, O., Cut points and diffusive random walks in random environment. Ann. Inst. H. Poincaré Probab. Statist. 39(2003), no. 3, 527–555. http://dx.doi.org/10.1016/S0246-0203(02)00019-5 Google Scholar
[4] Guo, X. and Zeitouni, O., Quenched invariance principle for random walks in balanced random environment. Probab. Theory Related Field 152 (2012), 207–230. http://dx.doi.org/10.1007/s00440-010-0320-9 Google Scholar
[5] Holmes, M. and Salisbury, T.S., Degenerate random environments. To appear, Random Structures and Algorithms, 2012. http://dx.doi.org/10.1016/j.jcta.2011.10.004 Google Scholar
[6] Holmes, M., Forward clusters for degenerate random environments. submitted, 2013. arxiv:1307.2787 Google Scholar
[7] Holmes, M., A combinatorial result with applications to self-interacting random walks. J. Combin. Theory Ser. A 119(2012), no. 2, 460–475.http://dx.doi.org/10.1016/j.jcta.2011.10.004 Google Scholar
[8] Holmes, M., Speed calculations for random walks in degenerate random environments. arxiv:1304.7520.Google Scholar
[9] Holmes, M. and Sun, R., A monotonicity property for random walk in a partially random environment. Stochastic Process. Appl. 122(2012), no. 4, 1369–1396 http://dx.doi.org/10.1016/j.spa.2012.01.006.Google Scholar
[10] Kalikow, S. A., Generalized random walks in a random environment. Ann. Probab. 9(1981), no. 5, 753–768. http://dx.doi.org/10.1214/aop/1176994306 Google Scholar
[11] Lawler, G. F., Weak convergence of a random walk in a random environment. Comm. Math. Phys. 87(1982/83), no. 1, 81–87. http://dx.doi.org/10.1007/BF01211057 Google Scholar
[12] Madras, N. and Tanny, D., Oscillating random walk with a moving boundary. Israel J. Math. 88(1994), no. 1, 333–365. http://dx.doi.org/10.1007/BF02937518 Google Scholar
[13] Rassoul-Agha, F. and Seppäläinen, T., Ballistic random walk in a random environment with a forbidden direction. ALEA Lat. Am. J. Probab. Math. Stat. 1(2006), 111–147.Google Scholar
[14] Sznitman, A.-S. and Zerner, M., A law of large numbers for random walks in random environment. Ann. Probab. 27(1999), no. 4, 1851–1869. http://dx.doi.org/10.1214/aop/1022874818 Google Scholar
[15] Zeitouni, O., Random walks in random environment. In: Lectures on probability theory and statistics, Lecture Notes in Mathematics, 1837, Springer, Berlin, 2004, 189–312.Google Scholar
[16] Zerner, M. P. W., A non-ballistic law of large numbers for random walks in i.i.d. random environment. Electron. Comm. Probab. 7(2002), 191–197.Google Scholar
[17] Zerner, M. P. W., Multi-excited random walks on integers. Probab. Theory Related Fields 133(2005), no. 1, 98–122. http://dx.doi.org/10.1007/s00440-004-0417-0 Google Scholar
[18] Zerner, M. P. W., Recurrence and transience of excited random walks on Zd and strips. Electron. Comm. Probab. 11(2006), 118–128.Google Scholar
[19] Zerner, M. P. W., The zero-one law for planar random walks in i.i.d. random environments revisited. Electron. Comm. Probab. 12(2007), 326–335.Google Scholar
[20] Zerner, M.P.W. and Merkl, F., A zero-one law for planar random walks in random environment. Ann. Probab. 29(2001), no. 4, 1716–1732. http://dx.doi.org/10.1214/aop/1015345769 Google Scholar