Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-24T04:22:23.956Z Has data issue: false hasContentIssue false
  • English
  • Français

Recursive Colorings of Highly Recursive Graphs

Published online by Cambridge University Press:  20 November 2018

Henry A. Kierstead
Henry A. Kierstead*
Affiliation:
University of South Carolina, Columbia, South Carolina
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

One of the attractions of finite combinatorics is its explicit constructions. This paper is part of a program to enlarge the domain of finite combinatorics to certain infinite structures while preserving the explicit constructions of the smaller domain. The larger domain to be considered consists of the recursive structures. While recursive structures may be infinite they are still amenable to explicit constructions. In this paper we shall concentrate on recursive colorings of highly recursive graphs.

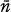A function f: Nk → N, where N is the set of natural numbers, is recursive if and only if there exists an algorithm (i.e., a finite computer program) which upon input of a sequence of natural numbers , after a finite number of steps, outputs 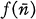. A subset of Nk is recursive provided that its characteristic function is recursive. For a more thorough definition of recursive functions and recursive relations see [10].

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 33 , Issue 6 , 01 December 1981 , pp. 1279 - 1290
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Bean, D., Effective coloration, J. Symbolic Logic 41 (1976), 469–480.Google Scholar
2. Brooks, R. L., On coloring nodes of a network, Proc. Cambridge Philos. Soc. 37 (1941), 194–197.Google Scholar
3. Dilworth, R. P., A decomposition theorem for partially ordered sets, Ann. of Math. 51 (1950), 161–166.Google Scholar
4. Ehrenfeucht, A., Faber, V. and Kierstead, H., A new method of proving theorems on chromatic index, in preparation.Google Scholar
5. Fiorini, S. and Wilson, R. J., Edge-colorings of graphs (Pitman, 1977).Google Scholar
6. Hall, P., On representatives of subsets, J. London Math. Soc. 10 (1935), 26–30.Google Scholar
7. Kierstead, H. A., An effective version of Dilworth's theorem, Trans. Amer. Math. Soc. 268 (1981), 63–77.Google Scholar
8. Kierstead, H. A. and Schmerl, J. H., Some applications of Vizing's Theorem to vertex colorings of graphs, in preparation.Google Scholar
9. Manaster, A. B. and Rosenstein, J. G., Effective matchmaking and k-chromatic graphs, Proc. Amer. Math. Soc. 39 (1973), 371–378.Google Scholar
10. Rodgers, H., Theory of recursive functions and effective computability (McGraw Hill, 1967).Google Scholar
11. Schmerl, J. H., Recursive colorings of graphs, to appear in Can. J. Math.Google Scholar
12. Schmerl, J. H., The effective version of Brooks 1 theorem, preprint.Google Scholar
13. Vizing, V. G., The chromatic class of a multigraph (in Russian), Kibernetika (kiev) 1 (1965), 29–39. English translation in Cybernetics (1965), 32-41.Google Scholar