Article contents
A Remark on Disintegrations With Almost All Components Non 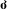 -Additive
-Additive
Published online by Cambridge University Press: 20 November 2018
Extract
We extend a theorem of L. E. Dubins on “purely finitely additive disintegrations” of measures (cf. [4]) and apply this result to the disintegrations of extremal Gibbs states with respect to the asymptotic algebra enlarging another result of L. E. Dubins on the symmetric coin tossing game.
We recall the following definition of L. E. Dubins (cf. [3], [4]): Let (X , 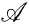 , μ) be a measure space,
, μ) be a measure space,  a sub σ-algebra of
a sub σ-algebra of 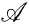 . A real function σx (A),
. A real function σx (A), 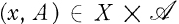 is called a measurable
is called a measurable -disintegration of μ if:
-disintegration of μ if:
-
(i) ∀x ∊ X , σx(.) is a finitely additive measure
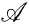 .
. -
(ii) ∀A ∊
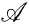 , σ. (A) is constant on each
, σ. (A) is constant on each  -atom.
-atom. -
(iii) For each A ∊
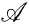 , σ. (A) is measurable with respect to the completion of
, σ. (A) is measurable with respect to the completion of 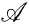 by μ and
by μ and 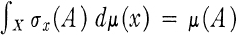
-
(iv) σx(B) = 1 if x ∊ B ∊
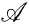 .
.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1979
References
- 1
- Cited by

