Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Myung, Hyo Chul
1972.
Some classes of flexible Lie-admissible algebras.
Transactions of the American Mathematical Society,
Vol. 167,
Issue. 0,
p.
79.
Myung, Hyo Chul
1976.
A subalgebra condition in Lie-admissible algebras.
Proceedings of the American Mathematical Society,
Vol. 59,
Issue. 1,
p.
6.
Jayalakshmi, K.
and
Devi, G. Lakshmi
2016.
On Vinberg ( − 1,1) rings.
Asian-European Journal of Mathematics,
Vol. 09,
Issue. 04,
p.
1650070.

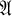
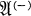
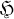 of
of 