Published online by Cambridge University Press: 20 November 2018
There is a well-known correspondence (due to Mehta and Seshadri in the unitary case, and extended by Bhosle and Ramanathan to other groups), between the symplectic variety 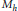 ${{M}_{h}}$ of representations of the fundamental group of a punctured Riemann surface into a compact connected Lie group
${{M}_{h}}$ of representations of the fundamental group of a punctured Riemann surface into a compact connected Lie group  $G$, with fixed conjugacy classes
$G$, with fixed conjugacy classes  $h$ at the punctures, and a complex variety
$h$ at the punctures, and a complex variety 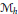 ${{\mathcal{M}}_{h}}$ of holomorphic bundles on the unpunctured surface with a parabolic structure at the puncture points. For
${{\mathcal{M}}_{h}}$ of holomorphic bundles on the unpunctured surface with a parabolic structure at the puncture points. For 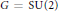 $G\,=\,\text{SU}\left( 2 \right)$, we build a symplectic variety
$G\,=\,\text{SU}\left( 2 \right)$, we build a symplectic variety  $P$ of pairs (representations of the fundamental group into
$P$ of pairs (representations of the fundamental group into  $G$, “weighted frame” at the puncture points), and a corresponding complex variety
$G$, “weighted frame” at the puncture points), and a corresponding complex variety 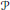 $\mathcal{P}$ of moduli of “framed parabolic bundles”, which encompass respectively all of the spaces
$\mathcal{P}$ of moduli of “framed parabolic bundles”, which encompass respectively all of the spaces 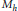 ${{M}_{h}}$,
${{M}_{h}}$, 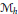 ${{\mathcal{M}}_{h}}$, in the sense that one can obtain
${{\mathcal{M}}_{h}}$, in the sense that one can obtain 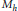 ${{M}_{h}}$ from
${{M}_{h}}$ from  $P$ by symplectic reduction, and
$P$ by symplectic reduction, and 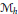 ${{\mathcal{M}}_{h}}$ from
${{\mathcal{M}}_{h}}$ from 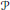 $\mathcal{P}$ by a complex quotient. This allows us to explain certain features of the toric geometry of the
$\mathcal{P}$ by a complex quotient. This allows us to explain certain features of the toric geometry of the 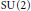 $\text{SU(2)}$ moduli spaces discussed by Jeffrey and Weitsman, by giving the actual toric variety associated with their integrable system.
$\text{SU(2)}$ moduli spaces discussed by Jeffrey and Weitsman, by giving the actual toric variety associated with their integrable system.