Hostname: page-component-7479d7b7d-fwgfc Total loading time: 0 Render date: 2024-07-09T19:52:48.590Z Has data issue: false hasContentIssue false
  • English
  • Français

The Resolvent of Closed Extensions of Cone Differential Operators

Published online by Cambridge University Press:  20 November 2018

E. Schrohe  and
J. Seiler
E. Schrohe
Affiliation:
Institut für Mathematik, Universität Hannover, Welfengarten 1, 30167 Hannover, Germany, e-mail: schrohe@math.uni-hannover.de
J. Seiler
Affiliation:
Institut für Angewandte Mathematik, Universität Hannover, Welfengarten 1, 30167 Hannover, Germany, e-mail: seiler@ifam.uni-hannover.de
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

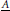We study closed extensions $\underset{\scriptscriptstyle-}{A}$ of an elliptic differential operator $A$ on a manifold with conical singularities, acting as an unbounded operator on a weighted 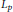${{L}_{p}}$-space. Under suitable conditions we show that the resolvent 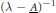${{\left( \lambda -\underset{\scriptscriptstyle-}{A} \right)}^{-1}}$ exists in a sector of the complex plane and decays like 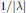$1/\left| \lambda \right|$ as 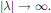$\left| \lambda \right|\to \infty $. Moreover, we determine the structure of the resolvent with enough precision to guarantee existence and boundedness of imaginary powers of 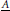$\underset{\scriptscriptstyle-}{A}$.

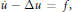As an application we treat the Laplace–Beltrami operator for a metric with straight conical degeneracy and describe domains yielding maximal regularity for the Cauchy problem $\dot{u}\,-\,\Delta u\,=\,f,$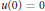$u\left( 0 \right)\,=\,0$.

Keywords

35J7047A1058J40Manifolds with conical singularitiesresolventmaximal regularity
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 57 , Issue 4 , 01 August 2005 , pp. 771 - 811
Copyright
Copyright © Canadian Mathematical Society 2005

References

[1] Brüning, J. and Seeley, R., An index theorem for first order regular singular operators. Amer. J. Math. 110(1988), 659–714.Google Scholar
[2] Cheeger, J., On the spectral geometry of spaces with cone-like singularities. Proc. Nat. Acad. Sci. U.S.A. 76(1979), 2103–2106.Google Scholar
[3] Coriasco, S., Schrohe, E., and Seiler, J., Bounded imaginary powers of differential operators on manifolds with conical singularities. Math. Z. 244(2003), 235–269.Google Scholar
[4] Coriasco, S., Schrohe, E., and Seiler, J., Differential operators on conic manifolds: maximal regularity and parabolic equations. Bull. Soc. Roy. Sci. Liège 70(2001), 207–229.Google Scholar
[5] Dore, G. and Venni, A., On the closednes of the sum of two closed operators. Math. Z. 196(1987), 189–201.Google Scholar
[6] Yu. Egorov, Schulze, B.-W., Pseudo-differential Operators, Singularities, Applications. Birkhäuser Verlag, Basel, 1997.Google Scholar
[7] Gil, J. B., Heat Trace Asymptotics for Cone Differential Operators. Ph.D. thesis, Potsdam, 1998.Google Scholar
[8] Gil, J. B., Full asymptotic expansion of the heat trace for non-self-adjoint elliptic cone operators. Math. Nachr. 250(2003), 25–57.Google Scholar
[9] Gil, J. B., and Loya, P., On the noncommutative residue and the heat trace expansion on conic manifolds. Manuscripta Math. 109(2002), 309–327.Google Scholar
[10] Gil, J. B. and Mendoza, G. A., Adjoints of elliptic cone operators. Amer. J. Math. 125(2003), 357–408.Google Scholar
[11] Gil, J. B., Schulze, B.-W., and Seiler, J., Cone pseudodifferential operators in the edge symbolic calculus. Osaka J. Math. 37(2000), 221–260.Google Scholar
[12] Lesch, M., Operators of Fuchs type, Conical Singularities, and Asymptotic Methods. Teubner-Texte zur Mathematik 136, Teubner-Verlag, Stuttgart, 1997.Google Scholar
[13] Loya, P., Complex powers of differential operators on manifolds with conical singularities. J. Anal. Math. 89(2003), 31–56.Google Scholar
[14] Loya, P., On the resolvent of differential operators on conic manifolds. Comm. Anal. Geom. 10(2002), 877–934.Google Scholar
[15] Melrose, R., Transformation of boundary problems. Acta Math. 147(1981), 149–236.Google Scholar
[16] Mooers, E., Heat kernel asymptotics on manifolds with conic singularities. J. Anal. Math. 78(1999), 1–36.Google Scholar
[17] Plamenevskij, B., Algebras of pseudodifferential operators. Nauka, Moscow, 1986 (in Russian).Google Scholar
[18] Schrohe, E., Spaces of weighted symbols and weighted Sobolev spaces on manifolds. In: Pseudodifferential Operators (Cordes, H. O., Gramsch, B., and H.Widom, eds.), Lecture Notes in Math. 1256, Springer, Berlin, 1987, pp. 360–377.Google Scholar
[19] Schrohe, E. and Schulze, B.-W., Edge-degenerate boundary value problems on cones. In: Evolution Equations and Their Applications in Physical and Life Sciences, Lecture Notes in Pure and Appl. Math. 215, Dekker, New York, 2001, pp. 159–173.Google Scholar
[20] Schrohe, E. and Seiler, J., Ellipticity and invertibility in the cone algebra on Lp-Sobolev spaces. Integral Equations Operator Theory 41(2001), 93–114.Google Scholar
[21] Schulze, B.-W., The Mellin pseudo-differential calculus on manifolds with corners. In: Symposium “Analysis onManifolds with Singularities” (Triebel, H. et al., eds.), Teubner-Texte zur Mathematik 131, Teubner-Verlag, Stuttgart, 1992, pp. 208–289.Google Scholar
[22] Schulze, B.-W., Pseudo-Differential Operators on Manifolds with Singularities. Studies in Mathematics and its Applications 24, North-Holland, Amsterdam, 1991.Google Scholar
[23] Seeley, R., Complex powers of an elliptic operator. In: Singular Integrals, American Mathematical Society, Providence, RI, 1967, pp. 288–307.Google Scholar
[24] Seeley, R. The resolvent of an elliptic boundary problem. Amer. J. Math. 91(1969), 889–920.Google Scholar
[25] Seeley, R., Norms and domains of the complex powers Az B. Amer. J. Math. 93(1971), 299–309.Google Scholar
[26] Seiler, J., Pseudodifferential Calculus on Manifolds with Non-compact Edges. Ph.D. thesis, Institut für Mathematik, Potsdam, 1997.Google Scholar
[27] Seiler, J., The cone algebra and a kernel characterization of Green operators. In: Approaches to Singular Analysis (Gil, J. B. et al., eds.), Oper. Theory Adv. Appl. 125, Birkhäuser, Basel, 2001, pp. 1–29.Google Scholar