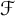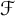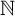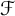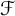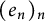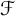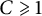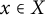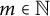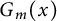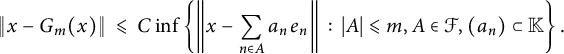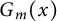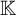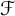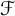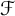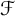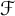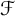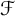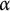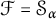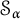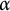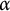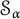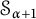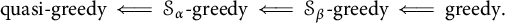1 Introduction
A (semi-normalized) basis in a Banach space X over the field
![]() $\mathbb {K}$
is a countable collection
$\mathbb {K}$
is a countable collection
![]() $(e_n)_n$
such that:
$(e_n)_n$
such that:
-
(i)
 $\overline {\operatorname {\mathrm {span}}\{e_n: n\in \mathbb {N}\}} = X$
,
$\overline {\operatorname {\mathrm {span}}\{e_n: n\in \mathbb {N}\}} = X$
, -
(ii) there exists a unique sequence
 $(e_n^*)_n\subset X^*$
such that
$(e_n^*)_n\subset X^*$
such that
 $e_i^*(e_j) = \delta _{i, j}$
for all
$e_i^*(e_j) = \delta _{i, j}$
for all
 $i, j\in \mathbb {N}$
, and
$i, j\in \mathbb {N}$
, and -
(iii) there exist
 $c_1, c_2> 0$
such that
$c_1, c_2> 0$
such that  $$ \begin{align*} 0 \ <\ c_1 := \inf_n\{\|e_n\|, \|e_n^*\|\}\ \leqslant\ \sup_n\{\|e_n\|, \|e_n^*\|\} \ =:\ c_2 \ <\ \infty. \end{align*} $$
$$ \begin{align*} 0 \ <\ c_1 := \inf_n\{\|e_n\|, \|e_n^*\|\}\ \leqslant\ \sup_n\{\|e_n\|, \|e_n^*\|\} \ =:\ c_2 \ <\ \infty. \end{align*} $$
In 1999, Konyagin and Temlyakov [Reference Konyagin and Temlyakov15] introduced the thresholding greedy algorithm (TGA), which picks the largest coefficients (in modulus) for the approximation. In particular, for each
![]() $x\in X$
and
$x\in X$
and
![]() $m\in \mathbb {N}$
, a set
$m\in \mathbb {N}$
, a set
![]() $\Lambda _m(x)$
is a greedy set of order m if
$\Lambda _m(x)$
is a greedy set of order m if
![]() ${|\Lambda _m(x)| = m}$
and
${|\Lambda _m(x)| = m}$
and
![]() $\min _{n\in \Lambda _m(x)}|e_n^*(x)|\geqslant \max _{n\notin \Lambda _m(x)}|e_n^*(x)|$
. A greedy operator
$\min _{n\in \Lambda _m(x)}|e_n^*(x)|\geqslant \max _{n\notin \Lambda _m(x)}|e_n^*(x)|$
. A greedy operator
![]() $G_m: X \to X$
is defined as
$G_m: X \to X$
is defined as
Note that
![]() $\Lambda _m(x)$
(and thus,
$\Lambda _m(x)$
(and thus,
![]() $G_m(x)$
) may not be unique and
$G_m(x)$
) may not be unique and
![]() $G_m$
is not even linear. The TGA is a sequence of greedy operators
$G_m$
is not even linear. The TGA is a sequence of greedy operators
![]() $(G_m)_{m=1}^{\infty }$
that gives the corresponding sequence of approximants
$(G_m)_{m=1}^{\infty }$
that gives the corresponding sequence of approximants
![]() $(G_m(x))_{m=1}^{\infty }$
for each
$(G_m(x))_{m=1}^{\infty }$
for each
![]() $x\in X$
.
$x\in X$
.
A basis
![]() $(e_n)_n$
for a Banach space X is called greedy if there is a
$(e_n)_n$
for a Banach space X is called greedy if there is a
![]() $C\geqslant 1$
such that for all
$C\geqslant 1$
such that for all
![]() $x\in X,m\in \mathbb {N}$
, and
$x\in X,m\in \mathbb {N}$
, and
![]() $G_m$
,
$G_m$
,
 $$ \begin{align*} \|x - G_m(x)\| \ \leqslant\ \ C \inf\left\{\left\|x-\sum_{n\in A}a_ne_n\right\|\,:\, |A|\leqslant m, (a_n)\subset \mathbb{K}\right\}. \end{align*} $$
$$ \begin{align*} \|x - G_m(x)\| \ \leqslant\ \ C \inf\left\{\left\|x-\sum_{n\in A}a_ne_n\right\|\,:\, |A|\leqslant m, (a_n)\subset \mathbb{K}\right\}. \end{align*} $$
A basis is called quasi-greedy [Reference Konyagin and Temlyakov15] if there is a
![]() $C\geqslant 1$
so that for all
$C\geqslant 1$
so that for all
![]() $x\in X, m\in \mathbb {N}$
, and
$x\in X, m\in \mathbb {N}$
, and
![]() $G_m$
, we have
$G_m$
, we have
![]() $\|G_m(x)\| \leqslant C\|x\|$
. The smallest such C is denoted by
$\|G_m(x)\| \leqslant C\|x\|$
. The smallest such C is denoted by
![]() ${\mathbf C}_w$
, called the quasi-greedy constant. Also, for quasi-greedy bases, let
${\mathbf C}_w$
, called the quasi-greedy constant. Also, for quasi-greedy bases, let
![]() ${\mathbf C}_{\ell }$
, called the suppression quasi-greedy constant, be the smallest constant such that
${\mathbf C}_{\ell }$
, called the suppression quasi-greedy constant, be the smallest constant such that
There are many examples of quasi-greedy bases that are not greedy (see [Reference Albiac and Kalton2, Example 10.2.9]), and there has been research on the existence of greedy bases for certain classical spaces [Reference Dilworth, Freeman, Odell and Schlumprecht13, Reference Schechtman17].
In this paper, we introduce and study the notion of what we call
![]() $\mathcal {F}$
-greedy bases which interpolate between greedy bases and quasi-greedy bases. Recall that a collection
$\mathcal {F}$
-greedy bases which interpolate between greedy bases and quasi-greedy bases. Recall that a collection
![]() $\mathcal {F}$
of finite subsets of
$\mathcal {F}$
of finite subsets of
![]() $\mathbb {N}$
is said to be hereditary if
$\mathbb {N}$
is said to be hereditary if
![]() $F\in \mathcal {F}$
and
$F\in \mathcal {F}$
and
![]() $G \subset F$
imply
$G \subset F$
imply
![]() $G \in \mathcal {F}$
.
$G \in \mathcal {F}$
.
Definition 1.1 Let
![]() $\mathcal {F}$
be a hereditary collection of finite subsets of
$\mathcal {F}$
be a hereditary collection of finite subsets of
![]() $\mathbb {N}$
. A basis
$\mathbb {N}$
. A basis
![]() $(e_n)_n$
is
$(e_n)_n$
is
![]() $\mathcal {F}$
-greedy if there exists a constant
$\mathcal {F}$
-greedy if there exists a constant
![]() $C\geqslant 1$
such that for all
$C\geqslant 1$
such that for all
![]() $x\in X,m\in \mathbb {N}$
, and
$x\in X,m\in \mathbb {N}$
, and
![]() $G_m$
,
$G_m$
,
where
 $$ \begin{align*} \sigma_m^{\mathcal{F}}(x)\ := \inf\left\{\left\|x-\sum_{n\in A}a_ne_n\right\|\,:\, |A|\leqslant m, A\in \mathcal{F}, (a_n)\subset \mathbb{K}\right\}. \end{align*} $$
$$ \begin{align*} \sigma_m^{\mathcal{F}}(x)\ := \inf\left\{\left\|x-\sum_{n\in A}a_ne_n\right\|\,:\, |A|\leqslant m, A\in \mathcal{F}, (a_n)\subset \mathbb{K}\right\}. \end{align*} $$
The least constant C is denoted by
![]() $\mathbf {C}_g^{\mathcal {F}}$
.
$\mathbf {C}_g^{\mathcal {F}}$
.
Remark 1.2 In the case when
![]() $\mathcal {F}=\mathcal {P}(\mathbb {N})$
,
$\mathcal {F}=\mathcal {P}(\mathbb {N})$
,
![]() $\mathcal {F}$
-greedy corresponds to greedy, and when
$\mathcal {F}$
-greedy corresponds to greedy, and when
![]() $\mathcal {F}=\{\emptyset \}$
,
$\mathcal {F}=\{\emptyset \}$
,
![]() $\mathcal {F}$
-greedy corresponds to quasi-greedy.
$\mathcal {F}$
-greedy corresponds to quasi-greedy.
The first order of business is to generalize the theorem of Konyagin and Temlyakov, which characterizes greedy bases as being unconditional and democratic. To do so, we introduce the definitions of
![]() $\mathcal {F}$
-unconditionality and
$\mathcal {F}$
-unconditionality and
![]() $\mathcal {F}$
-democracy. For various families
$\mathcal {F}$
-democracy. For various families
![]() $\mathcal {F}$
, the notion of
$\mathcal {F}$
, the notion of
![]() $\mathcal {F}$
-unconditionality has appeared numerous times in the literature, most notably in Odell’s result [Reference Odell16], which states that every normalized weakly null sequence in a Banach space has a subsequence that is Schreier-unconditional. Also, see [Reference Argyros and Gasparis5–Reference Argyros, Mercourakis and Tsarpalias7] for other notion of unconditionality for weakly null sequences.
$\mathcal {F}$
-unconditionality has appeared numerous times in the literature, most notably in Odell’s result [Reference Odell16], which states that every normalized weakly null sequence in a Banach space has a subsequence that is Schreier-unconditional. Also, see [Reference Argyros and Gasparis5–Reference Argyros, Mercourakis and Tsarpalias7] for other notion of unconditionality for weakly null sequences.
For a basis
![]() $(e_n)_n$
of a Banach space X and a finite set
$(e_n)_n$
of a Banach space X and a finite set
![]() $A \subset \mathbb {N}$
, let
$A \subset \mathbb {N}$
, let
![]() $P_A: X \to X$
be defined by
$P_A: X \to X$
be defined by
![]() $P_A(\sum _i e^*_i(x) e_i)=\sum _{i\in A} e^*_i(x) e_i$
.
$P_A(\sum _i e^*_i(x) e_i)=\sum _{i\in A} e^*_i(x) e_i$
.
Definition 1.3 A basis
![]() $(e_n)$
of a Banach space X is
$(e_n)$
of a Banach space X is
![]() $\mathcal {F}$
-unconditional if there exists a constant
$\mathcal {F}$
-unconditional if there exists a constant
![]() $C\geqslant 1$
such that for each
$C\geqslant 1$
such that for each
![]() $x \in X$
and
$x \in X$
and
![]() $A \in \mathcal {F}$
, we have
$A \in \mathcal {F}$
, we have
The least constant C is denoted by
![]() ${\mathbf K}_s^{\mathcal {F}}$
. We say that
${\mathbf K}_s^{\mathcal {F}}$
. We say that
![]() $(e_n)$
is
$(e_n)$
is
![]() ${\mathbf K}_s^{\mathcal {F}}$
-
${\mathbf K}_s^{\mathcal {F}}$
-
![]() $\mathcal {F}$
-suppression unconditional.
$\mathcal {F}$
-suppression unconditional.
As far as we know, the following natural definition has not appeared in the literature before.
Definition 1.4 A basis
![]() $(e_n)$
is
$(e_n)$
is
![]() $\mathcal {F}$
-disjoint democratic (
$\mathcal {F}$
-disjoint democratic (
![]() $\mathcal {F}$
-disjoint superdemocratic, respectively) if there exists a constant
$\mathcal {F}$
-disjoint superdemocratic, respectively) if there exists a constant
![]() $C\geqslant 1$
such that
$C\geqslant 1$
such that
 $$ \begin{align*} \left\|\sum_{i\in A}e_i\right\|\ \leqslant \ C\left\|\sum_{i\in B}e_i\right\| \mbox{ }\left(\left\|\sum_{i\in A}\varepsilon_i e_i\right\|\ \leqslant\ C\left\|\sum_{i\in B} \delta_i e_i\right\|,\mbox{ respectively}\right), \end{align*} $$
$$ \begin{align*} \left\|\sum_{i\in A}e_i\right\|\ \leqslant \ C\left\|\sum_{i\in B}e_i\right\| \mbox{ }\left(\left\|\sum_{i\in A}\varepsilon_i e_i\right\|\ \leqslant\ C\left\|\sum_{i\in B} \delta_i e_i\right\|,\mbox{ respectively}\right), \end{align*} $$
for all finite sets
![]() $A, B\subset \mathbb {N}$
with
$A, B\subset \mathbb {N}$
with
![]() $A\in \mathcal {F}$
,
$A\in \mathcal {F}$
,
![]() $|A|\leqslant |B|, A\cap B = \emptyset $
, and signs
$|A|\leqslant |B|, A\cap B = \emptyset $
, and signs
![]() $(\varepsilon _i), (\delta _i)$
. The least constant C is denoted by
$(\varepsilon _i), (\delta _i)$
. The least constant C is denoted by
![]() ${\mathbf C}^{\mathcal {F}}_{d,\sqcup }$
${\mathbf C}^{\mathcal {F}}_{d,\sqcup }$
![]() ${\mathbf C}^{\mathcal {F}}_{sd,\sqcup }$
, respectively. When
${\mathbf C}^{\mathcal {F}}_{sd,\sqcup }$
, respectively. When
![]() $\mathcal {F} = \mathcal {P}(\mathbb {N})$
, we say that
$\mathcal {F} = \mathcal {P}(\mathbb {N})$
, we say that
![]() $(e_n)$
is (super)democratic.
$(e_n)$
is (super)democratic.
One of our main results is the following generalization of the Konyagin–Temlyakov theorem [Reference Konyagin and Temlyakov15].
Theorem 1.5 A basis
![]() $(e_n)$
in a Banach space X is
$(e_n)$
in a Banach space X is
![]() $\mathcal {F}$
-greedy if and only if it is quasi-greedy,
$\mathcal {F}$
-greedy if and only if it is quasi-greedy,
![]() $\mathcal {F}$
-unconditional, and
$\mathcal {F}$
-unconditional, and
![]() $\mathcal {F}$
-disjoint democratic.
$\mathcal {F}$
-disjoint democratic.
We also present another characterization regarding
![]() $\mathcal {F}$
-almost greedy bases.
$\mathcal {F}$
-almost greedy bases.
Definition 1.6 A basis
![]() $(e_n)$
is
$(e_n)$
is
![]() $\mathcal {F}$
-almost greedy if there exists a constant
$\mathcal {F}$
-almost greedy if there exists a constant
![]() $C\geqslant 1$
such that for all
$C\geqslant 1$
such that for all
![]() $x \in X, m\in \mathbb {N}$
, and
$x \in X, m\in \mathbb {N}$
, and
![]() $G_m$
, we have
$G_m$
, we have
The least constant C is denoted by
![]() $\mathbf {C}_a^{\mathcal {F}}$
.
$\mathbf {C}_a^{\mathcal {F}}$
.
The next theorem generalizes [Reference Dilworth, Kalton, Kutzarova and Temlyakov14, Theorem 3.3].
Theorem 1.7 A basis
![]() $(e_n)$
is
$(e_n)$
is
![]() $\mathcal {F}$
-almost greedy if and only if it is quasi-greedy and
$\mathcal {F}$
-almost greedy if and only if it is quasi-greedy and
![]() $\mathcal {F}$
-disjoint democratic.
$\mathcal {F}$
-disjoint democratic.
The second set of results in this paper focuses on the well-known Schreier families
![]() $(\mathcal {S}_{\alpha })_{n=1}^{\infty }$
(for each countable ordinal
$(\mathcal {S}_{\alpha })_{n=1}^{\infty }$
(for each countable ordinal
![]() $\alpha $
) introduced by Alspach and Argyros [Reference Alspach and Argyros4]. The sequence of countable ordinals is
$\alpha $
) introduced by Alspach and Argyros [Reference Alspach and Argyros4]. The sequence of countable ordinals is
We recall the definition of
![]() $\mathcal {S}_{\alpha }$
. For two sets
$\mathcal {S}_{\alpha }$
. For two sets
![]() $A, B\subset \mathbb {N}$
, we write
$A, B\subset \mathbb {N}$
, we write
![]() $A < B$
to mean that
$A < B$
to mean that
![]() $a < b$
for all
$a < b$
for all
![]() $a\in A, b\in B$
. It holds vacuously that
$a\in A, b\in B$
. It holds vacuously that
![]() $\emptyset < A$
and
$\emptyset < A$
and
![]() $\emptyset> A$
. Also,
$\emptyset> A$
. Also,
![]() $n < A$
for a number n means
$n < A$
for a number n means
![]() $\{n\} < A$
. Let
$\{n\} < A$
. Let
![]() $\mathcal {S}_0$
be the set of singletons and the empty set. Supposing that
$\mathcal {S}_0$
be the set of singletons and the empty set. Supposing that
![]() $\mathcal {S}_{\alpha }$
has to be defined for some ordinal
$\mathcal {S}_{\alpha }$
has to be defined for some ordinal
![]() $\alpha \geqslant 0$
, we define
$\alpha \geqslant 0$
, we define
If
![]() $\alpha $
is a limit ordinal, then fix
$\alpha $
is a limit ordinal, then fix
![]() $\alpha _{m}+1\nearrow \alpha $
with
$\alpha _{m}+1\nearrow \alpha $
with
![]() $\mathcal {S}_{\alpha _{m}}\subset \mathcal {S}_{\alpha _{m+1}}$
for all
$\mathcal {S}_{\alpha _{m}}\subset \mathcal {S}_{\alpha _{m+1}}$
for all
![]() $m\geqslant 1$
and define
$m\geqslant 1$
and define
The following proposition is well known, but we include its proof for completion.
Proposition 1.8 Let
![]() $\alpha < \beta $
be two countable ordinals. There exists
$\alpha < \beta $
be two countable ordinals. There exists
![]() $N\in \mathbb {N}$
such that
$N\in \mathbb {N}$
such that
Proof Fix two ordinals
![]() $\alpha < \beta $
. We prove by induction. Base cases: if
$\alpha < \beta $
. We prove by induction. Base cases: if
![]() $\beta = 0$
, there is nothing to prove. If
$\beta = 0$
, there is nothing to prove. If
![]() $\beta = 1$
, then
$\beta = 1$
, then
![]() $\alpha = 0$
. Clearly,
$\alpha = 0$
. Clearly,
![]() $\mathcal {S}_0\subset \mathcal {S}_1$
. Inductive hypothesis: suppose that the proposition holds for all
$\mathcal {S}_0\subset \mathcal {S}_1$
. Inductive hypothesis: suppose that the proposition holds for all
![]() $\eta < \beta $
. If
$\eta < \beta $
. If
![]() $\beta $
is a successor ordinal, then write
$\beta $
is a successor ordinal, then write
![]() $\beta = \gamma + 1$
. Since
$\beta = \gamma + 1$
. Since
![]() $\alpha < \beta $
, we have
$\alpha < \beta $
, we have
![]() $\alpha \leqslant \gamma $
. By the inductive hypothesis, there exists
$\alpha \leqslant \gamma $
. By the inductive hypothesis, there exists
![]() $N\in \mathbb {N}$
such that
$N\in \mathbb {N}$
such that
By definition,
![]() $\mathcal {S}_{\gamma }\subset \mathcal {S}_{\beta }$
. Hence,
$\mathcal {S}_{\gamma }\subset \mathcal {S}_{\beta }$
. Hence,
If
![]() $\beta $
is a limit ordinal, then let
$\beta $
is a limit ordinal, then let
![]() $\beta _m\nearrow \beta $
. There exists
$\beta _m\nearrow \beta $
. There exists
![]() $M\in \mathbb {N}$
such that
$M\in \mathbb {N}$
such that
![]() $\beta _M\geqslant \alpha $
. By the inductive hypothesis, there exists
$\beta _M\geqslant \alpha $
. By the inductive hypothesis, there exists
![]() $N_1\in \mathbb {N}$
such that
$N_1\in \mathbb {N}$
such that
By definition,
Therefore,
This completes our proof.
We have the following corollary, which is proved in Section 4.
Corollary 1.9 For two countable ordinals
![]() $\alpha < \beta $
, an
$\alpha < \beta $
, an
![]() $\mathcal {S}_{\beta }$
-greedy basis is
$\mathcal {S}_{\beta }$
-greedy basis is
![]() $\mathcal {S}_{\alpha }$
-greedy.
$\mathcal {S}_{\alpha }$
-greedy.
Each Schreier family
![]() $\mathcal {S}_{\alpha }$
is obviously hereditary and is moreover spreading and compact (see [Reference Argyros, Godefroy, Rosenthal, Johnson and Lindenstrauss6, pp. 1049 and 1051]). We shall show that each of the following implications cannot be reversed: for two countable ordinals
$\mathcal {S}_{\alpha }$
is obviously hereditary and is moreover spreading and compact (see [Reference Argyros, Godefroy, Rosenthal, Johnson and Lindenstrauss6, pp. 1049 and 1051]). We shall show that each of the following implications cannot be reversed: for two countable ordinals
![]() $\alpha < \beta $
,
$\alpha < \beta $
,
We, thereby, study the greedy counterpart of the notion of
![]() $\mathcal {S}_{\alpha }$
-unconditionality.
$\mathcal {S}_{\alpha }$
-unconditionality.
Theorem 1.10 For two countable ordinals
![]() $\alpha < \beta $
, there exists a Banach space X with an
$\alpha < \beta $
, there exists a Banach space X with an
![]() $\mathcal {S}_{\alpha }$
-greedy basis that is not
$\mathcal {S}_{\alpha }$
-greedy basis that is not
![]() $\mathcal {S}_{\beta }$
-greedy.
$\mathcal {S}_{\beta }$
-greedy.
Theorem 1.11 Fix a countable ordinal
![]() $\alpha $
.
$\alpha $
.
-
(1) A basis is greedy if and only if it is C-
 $\mathcal {S}_{\alpha +m}$
-greedy for all
$\mathcal {S}_{\alpha +m}$
-greedy for all
 $m\in \mathbb {N}$
and some uniform
$m\in \mathbb {N}$
and some uniform
 $C\geqslant 1$
.
$C\geqslant 1$
. -
(2) There exists a basis that is
 $\mathcal {S}_{\alpha +m}$
-greedy (with different constants) for all
$\mathcal {S}_{\alpha +m}$
-greedy (with different constants) for all
 $m\in \mathbb {N}$
but is not greedy.
$m\in \mathbb {N}$
but is not greedy.
2 Characterizations of
 $\mathcal {F}$
-greedy bases
$\mathcal {F}$
-greedy bases
In this section, we prove Theorem 1.5 and other characterizations of
![]() $\mathcal {F}$
-greedy bases. Throughout,
$\mathcal {F}$
-greedy bases. Throughout,
![]() $\mathcal {F}$
will be a hereditary family of finite subsets of
$\mathcal {F}$
will be a hereditary family of finite subsets of
![]() $\mathbb {N}$
. We first need to define Property (A,
$\mathbb {N}$
. We first need to define Property (A,
![]() $\mathcal {F}$
), inspired by the classical Property (A) introduced by Albiac and Wojtaszczyk in [Reference Albiac and Wojtaszczyk3]. Write
$\mathcal {F}$
), inspired by the classical Property (A) introduced by Albiac and Wojtaszczyk in [Reference Albiac and Wojtaszczyk3]. Write
![]() $\sqcup _{i\in I} A_i$
, for some index set I and sets
$\sqcup _{i\in I} A_i$
, for some index set I and sets
![]() $(A_i)_{i\in I}$
, to mean that the
$(A_i)_{i\in I}$
, to mean that the
![]() $A_i$
’s are pairwise disjoint. Define
$A_i$
’s are pairwise disjoint. Define
![]() $1_A = \sum _{n\in A}e_n\mbox { and }1_{\varepsilon A} = \sum _{n\in A}\varepsilon _n e_n$
, for some signs
$1_A = \sum _{n\in A}e_n\mbox { and }1_{\varepsilon A} = \sum _{n\in A}\varepsilon _n e_n$
, for some signs
![]() $(\varepsilon ) = (\varepsilon _n)_n\in \mathbb {K}^{\mathbb {N}}$
.
$(\varepsilon ) = (\varepsilon _n)_n\in \mathbb {K}^{\mathbb {N}}$
.
Definition 2.1 A basis
![]() $(e_n)$
is said to have Property (A,
$(e_n)$
is said to have Property (A,
![]() $\mathcal {F}$
) if there exists a constant
$\mathcal {F}$
) if there exists a constant
![]() $C\geqslant 1$
such that
$C\geqslant 1$
such that
 $$ \begin{align*}\left\|x+\sum_{i \in A} \varepsilon_i e_i\right\|\ \leqslant\ C\left\|x + \sum_{n\in B}b_n e_n\right\|,\end{align*} $$
$$ \begin{align*}\left\|x+\sum_{i \in A} \varepsilon_i e_i\right\|\ \leqslant\ C\left\|x + \sum_{n\in B}b_n e_n\right\|,\end{align*} $$
for all
![]() $x\in X$
with
$x\in X$
with
![]() $\|x\|_{\infty }\leqslant 1$
, for all finite sets
$\|x\|_{\infty }\leqslant 1$
, for all finite sets
![]() $A, B\subset \mathbb {N}$
with
$A, B\subset \mathbb {N}$
with
![]() $|A|\leqslant |B|$
,
$|A|\leqslant |B|$
,
![]() $A\in \mathcal {F}$
,
$A\in \mathcal {F}$
,
![]() $A\sqcup B\sqcup \operatorname {\mathrm {supp}}(x)$
, and for all signs
$A\sqcup B\sqcup \operatorname {\mathrm {supp}}(x)$
, and for all signs
![]() $(\varepsilon _i)$
and
$(\varepsilon _i)$
and
![]() $|b_n|\geqslant 1$
. The least constant C is denoted by
$|b_n|\geqslant 1$
. The least constant C is denoted by
![]() ${\mathbf C}^{\mathcal {F}}_b$
.
${\mathbf C}^{\mathcal {F}}_b$
.
Proposition 2.2 A basis
![]() $(e_n)$
has
$(e_n)$
has
![]() ${\mathbf C}^{\mathcal {F}}_{b}$
-Property (A,
${\mathbf C}^{\mathcal {F}}_{b}$
-Property (A,
![]() $\mathcal {F}$
) if and only if
$\mathcal {F}$
) if and only if
 $$ \begin{align} \|x\|\ \leqslant\ {\mathbf C}^{\mathcal{F}}_b \left\|x-P_A(x) + \sum_{n\in B}b_n e_n\right\|, \end{align} $$
$$ \begin{align} \|x\|\ \leqslant\ {\mathbf C}^{\mathcal{F}}_b \left\|x-P_A(x) + \sum_{n\in B}b_n e_n\right\|, \end{align} $$
for all
![]() $x\in X$
with
$x\in X$
with
![]() $\|x\|_{\infty }\leqslant 1$
, for all finite sets
$\|x\|_{\infty }\leqslant 1$
, for all finite sets
![]() $A, B\subset \mathbb {N}$
with
$A, B\subset \mathbb {N}$
with
![]() $|A|\leqslant |B|$
,
$|A|\leqslant |B|$
,
![]() $A\in \mathcal {F}$
,
$A\in \mathcal {F}$
,
![]() $B\cap (A\cup \operatorname {\mathrm {supp}}(x)) = \emptyset $
, and
$B\cap (A\cup \operatorname {\mathrm {supp}}(x)) = \emptyset $
, and
![]() $|b_n|\geqslant 1$
.
$|b_n|\geqslant 1$
.
Proof Assume (2.1). Let
![]() $x, A, B, (\varepsilon ), (b_n)_{n\in B}$
be as in Definition 2.1. Let
$x, A, B, (\varepsilon ), (b_n)_{n\in B}$
be as in Definition 2.1. Let
![]() $y = x + 1_{\varepsilon A}$
. By (2.1),
$y = x + 1_{\varepsilon A}$
. By (2.1),
 $$ \begin{align*} \|x+1_{\varepsilon A}\|\ =\ \|y\|\ \leqslant\ {\mathbf C}^{\mathcal{F}}_b\left\|y- P_A(y) + \sum_{n\in B}b_n e_n\right\|\ =\ {\mathbf C}^{\mathcal{F}}_b \left\|x+\sum_{n\in B}b_ne_n\right\|. \end{align*} $$
$$ \begin{align*} \|x+1_{\varepsilon A}\|\ =\ \|y\|\ \leqslant\ {\mathbf C}^{\mathcal{F}}_b\left\|y- P_A(y) + \sum_{n\in B}b_n e_n\right\|\ =\ {\mathbf C}^{\mathcal{F}}_b \left\|x+\sum_{n\in B}b_ne_n\right\|. \end{align*} $$
Conversely, assume that
![]() $(e_n)$
has
$(e_n)$
has
![]() ${\mathbf C}^{\mathcal {F}}_b$
-Property (A,
${\mathbf C}^{\mathcal {F}}_b$
-Property (A,
![]() $\mathcal {F}$
). Let
$\mathcal {F}$
). Let
![]() $x, A, B, (b_n)_{n\in B}$
be as in (2.1). We have
$x, A, B, (b_n)_{n\in B}$
be as in (2.1). We have
 $$ \begin{align*} \|x\|\ =\ \left\|x-P_A(x) + \sum_{n\in A}e_n^*(x)e_n\right\|&\ \leqslant\ \sup_{(\delta)}\left\|x-P_A(x) + 1_{\delta A}\right\|\mbox{ by norm convexity}\\ &\ \leqslant\ {\mathbf C}^{\mathcal{F}}_b\left\|x - P_A(x) + \sum_{n\in B}b_ne_n\right\|, \end{align*} $$
$$ \begin{align*} \|x\|\ =\ \left\|x-P_A(x) + \sum_{n\in A}e_n^*(x)e_n\right\|&\ \leqslant\ \sup_{(\delta)}\left\|x-P_A(x) + 1_{\delta A}\right\|\mbox{ by norm convexity}\\ &\ \leqslant\ {\mathbf C}^{\mathcal{F}}_b\left\|x - P_A(x) + \sum_{n\in B}b_ne_n\right\|, \end{align*} $$
where the last inequality is due to Property (A,
![]() $\mathcal {F}$
).
$\mathcal {F}$
).
Theorem 2.3 Let
![]() $(e_n)$
be a basis for a Banach space X.
$(e_n)$
be a basis for a Banach space X.
-
(1) The basis
 $(e_n)$
is
$(e_n)$
is
 ${\mathbf C}^{\mathcal {F}}_g$
-
${\mathbf C}^{\mathcal {F}}_g$
-
 $\mathcal {F}$
-greedy, then
$\mathcal {F}$
-greedy, then
 $(e_n)$
is
$(e_n)$
is
 ${\mathbf C}^{\mathcal {F}}_g$
-
${\mathbf C}^{\mathcal {F}}_g$
-
 $\mathcal {F}$
-suppression unconditional and has
$\mathcal {F}$
-suppression unconditional and has
 ${\mathbf C}^{\mathcal {F}}_g$
-Property (A,
${\mathbf C}^{\mathcal {F}}_g$
-Property (A,
 $\mathcal {F}$
).
$\mathcal {F}$
). -
(2) The basis
 $(e_n)$
is
$(e_n)$
is
 ${\mathbf K}^{\mathcal {F}}_s$
-
${\mathbf K}^{\mathcal {F}}_s$
-
 $\mathcal {F}$
-suppression unconditional and has
$\mathcal {F}$
-suppression unconditional and has
 ${\mathbf C}^{\mathcal {F}}_b$
-Property (A,
${\mathbf C}^{\mathcal {F}}_b$
-Property (A,
 $\mathcal {F}$
), then
$\mathcal {F}$
), then
 $(e_n)$
is
$(e_n)$
is
 ${\mathbf K}^{\mathcal {F}}_s{\mathbf C}^{\mathcal {F}}_b$
-
${\mathbf K}^{\mathcal {F}}_s{\mathbf C}^{\mathcal {F}}_b$
-
 $\mathcal {F}$
-greedy.
$\mathcal {F}$
-greedy.
Proof (1) Assume that
![]() $(e_n)$
is
$(e_n)$
is
![]() ${\mathbf C}^{\mathcal {F}}_g$
-
${\mathbf C}^{\mathcal {F}}_g$
-
![]() $\mathcal {F}$
-greedy. We shall show that
$\mathcal {F}$
-greedy. We shall show that
![]() $(e_n)$
is
$(e_n)$
is
![]() $\mathcal {F}$
-unconditional. Choose
$\mathcal {F}$
-unconditional. Choose
![]() $x\in X$
and a finite set
$x\in X$
and a finite set
![]() $B\in \mathcal {F}$
. Set
$B\in \mathcal {F}$
. Set
where
![]() $\alpha $
is sufficiently large such that B is a greedy set of y. Then
$\alpha $
is sufficiently large such that B is a greedy set of y. Then
Hence,
![]() $(e_n)$
is
$(e_n)$
is
![]() ${\mathbf C}^{\mathcal {F}}_g$
-
${\mathbf C}^{\mathcal {F}}_g$
-
![]() $\mathcal {F}$
-suppression unconditional.
$\mathcal {F}$
-suppression unconditional.
Next, we prove Property (A,
![]() $\mathcal {F}$
). Choose
$\mathcal {F}$
). Choose
![]() $x, A, B, (\varepsilon _i), (b_n)_{n\in B}$
as in Definition 2.1. Set
$x, A, B, (\varepsilon _i), (b_n)_{n\in B}$
as in Definition 2.1. Set
![]() $y:= x + 1_{\varepsilon A} + \sum _{n\in B}b_ne_n$
. Since B is a greedy set of y, we have
$y:= x + 1_{\varepsilon A} + \sum _{n\in B}b_ne_n$
. Since B is a greedy set of y, we have
 $$ \begin{align*} \|x+1_{\varepsilon A}\|\ =\ \|y-P_B(y)\|\ \leqslant\ {\mathbf C}_g^{\mathcal{F}}\sigma^{\mathcal{F}}_{|B|}(y)\ \leqslant\ {\mathbf C}_g^{\mathcal{F}}\|y-P_A(y)\|\ =\ {\mathbf C}_g^{\mathcal{F}}\left\|x+\sum_{n\in B}b_ne_n\right\|. \end{align*} $$
$$ \begin{align*} \|x+1_{\varepsilon A}\|\ =\ \|y-P_B(y)\|\ \leqslant\ {\mathbf C}_g^{\mathcal{F}}\sigma^{\mathcal{F}}_{|B|}(y)\ \leqslant\ {\mathbf C}_g^{\mathcal{F}}\|y-P_A(y)\|\ =\ {\mathbf C}_g^{\mathcal{F}}\left\|x+\sum_{n\in B}b_ne_n\right\|. \end{align*} $$
Therefore,
![]() $(e_n)$
has
$(e_n)$
has
![]() ${\mathbf C}_g^{\mathcal {F}}$
-Property (A,
${\mathbf C}_g^{\mathcal {F}}$
-Property (A,
![]() $\mathcal {F}$
).
$\mathcal {F}$
).
(2) Assume that
![]() $(e_n)$
is
$(e_n)$
is
![]() ${\mathbf K}^{\mathcal {F}}_s$
-
${\mathbf K}^{\mathcal {F}}_s$
-
![]() $\mathcal {F}$
-unconditional and has
$\mathcal {F}$
-unconditional and has
![]() ${\mathbf C}^{\mathcal {F}}_b$
-Property (A,
${\mathbf C}^{\mathcal {F}}_b$
-Property (A,
![]() $\mathcal {F}$
). Let
$\mathcal {F}$
). Let
![]() ${x\in X}$
with a greedy set A. Choose
${x\in X}$
with a greedy set A. Choose
![]() $B\in \mathcal {F}$
with
$B\in \mathcal {F}$
with
![]() $|B|\leqslant |A|$
and choose
$|B|\leqslant |A|$
and choose
![]() $(b_n)_{n\in B}\subset \mathbb {K}$
. If
$(b_n)_{n\in B}\subset \mathbb {K}$
. If
![]() ${A\backslash B = \emptyset }$
, then
${A\backslash B = \emptyset }$
, then
![]() $A = B$
, and we have
$A = B$
, and we have
 $$ \begin{align*} \|x-P_A(x)\|\ =\ \|x-P_B(x)\|&\ \leqslant\ {\mathbf K}^{\mathcal{F}}_s\left\|x-P_B(x) + \sum_{n\in B}(e_n^*(x)-b_n)e_n\right\|\\ &\ =\ {\mathbf K}^{\mathcal{F}}_s\left\|x - \sum_{n\in B}b_ne_n\right\|. \end{align*} $$
$$ \begin{align*} \|x-P_A(x)\|\ =\ \|x-P_B(x)\|&\ \leqslant\ {\mathbf K}^{\mathcal{F}}_s\left\|x-P_B(x) + \sum_{n\in B}(e_n^*(x)-b_n)e_n\right\|\\ &\ =\ {\mathbf K}^{\mathcal{F}}_s\left\|x - \sum_{n\in B}b_ne_n\right\|. \end{align*} $$
Assume that
![]() $A\backslash B\neq \emptyset $
. Note that
$A\backslash B\neq \emptyset $
. Note that
![]() $B\backslash A\in \mathcal {F}$
as
$B\backslash A\in \mathcal {F}$
as
![]() $\mathcal {F}$
is hereditary and
$\mathcal {F}$
is hereditary and
![]() $\min _{n\in A\backslash B}|e_n^*(x)|\geqslant \|x-P_A(x)\|_{\infty }$
. By Proposition 2.2, we have
$\min _{n\in A\backslash B}|e_n^*(x)|\geqslant \|x-P_A(x)\|_{\infty }$
. By Proposition 2.2, we have
 $$ \begin{align*} \|x-P_A(x)\|&\ \leqslant\ {\mathbf C}^{\mathcal{F}}_b\|(x-P_A(x)) - P_{B\backslash A}(x) + P_{A\backslash B}(x)\|\\ &\ =\ {\mathbf C}^{\mathcal{F}}_b\|x-P_B(x)\|\\ &\ \leqslant\ {\mathbf C}^{\mathcal{F}}_b{\mathbf K}^{\mathcal{F}}_s\left\|x-P_B(x) + \sum_{n\in B}(e_n^*(x)-b_n)e_n\right\|\\ &\ =\ {\mathbf C}^{\mathcal{F}}_b{\mathbf K}^{\mathcal{F}}_s\left\|x-\sum_{n\in B}b_ne_n\right\|. \end{align*} $$
$$ \begin{align*} \|x-P_A(x)\|&\ \leqslant\ {\mathbf C}^{\mathcal{F}}_b\|(x-P_A(x)) - P_{B\backslash A}(x) + P_{A\backslash B}(x)\|\\ &\ =\ {\mathbf C}^{\mathcal{F}}_b\|x-P_B(x)\|\\ &\ \leqslant\ {\mathbf C}^{\mathcal{F}}_b{\mathbf K}^{\mathcal{F}}_s\left\|x-P_B(x) + \sum_{n\in B}(e_n^*(x)-b_n)e_n\right\|\\ &\ =\ {\mathbf C}^{\mathcal{F}}_b{\mathbf K}^{\mathcal{F}}_s\left\|x-\sum_{n\in B}b_ne_n\right\|. \end{align*} $$
Since B and
![]() $(b_n)$
are arbitrary, we know that
$(b_n)$
are arbitrary, we know that
![]() $(e_n)$
is
$(e_n)$
is
![]() ${\mathbf C}^{\mathcal {F}}_b{\mathbf K}^{\mathcal {F}}_s$
-
${\mathbf C}^{\mathcal {F}}_b{\mathbf K}^{\mathcal {F}}_s$
-
![]() $\mathcal {F}$
-greedy.
$\mathcal {F}$
-greedy.
We have the following immediate corollary.
Corollary 2.4 A basis
![]() $(e_n)$
is
$(e_n)$
is
![]() $1$
-
$1$
-
![]() $\mathcal {F}$
-greedy if and only if it is
$\mathcal {F}$
-greedy if and only if it is
![]() $1$
-
$1$
-
![]() $\mathcal {F}$
-unconditional and has
$\mathcal {F}$
-unconditional and has
![]() $1$
-Property (A,
$1$
-Property (A,
![]() $\mathcal {F}$
).
$\mathcal {F}$
).
The next proposition connects Property
![]() $(A,\mathcal {F})$
and
$(A,\mathcal {F})$
and
![]() $\mathcal {F}$
-disjoint democracy.
$\mathcal {F}$
-disjoint democracy.
Proposition 2.5 Let
![]() $(e_n)$
be a quasi-greedy basis. Then
$(e_n)$
be a quasi-greedy basis. Then
![]() $(e_n)$
has Property (A,
$(e_n)$
has Property (A,
![]() $\mathcal {F}$
) if and only if
$\mathcal {F}$
) if and only if
![]() $(e_n)$
is
$(e_n)$
is
![]() $\mathcal {F}$
-disjoint democratic.
$\mathcal {F}$
-disjoint democratic.
The proof of Proposition 2.5 uses the following results which can be found in [Reference Wojtaszczyk18] and [Reference Berná, Blasco and Garrigós12, Lemma 2.5].
Lemma 2.6 Let
![]() $(e_n)$
be a
$(e_n)$
be a
![]() ${\mathbf C}_{\ell }$
-suppression quasi-greedy basis. The following hold:
${\mathbf C}_{\ell }$
-suppression quasi-greedy basis. The following hold:
-
(1) For any finite set
 $A\subset \mathbb {N}$
and sign
$A\subset \mathbb {N}$
and sign
 $(\varepsilon _n)_n$
, we have
$(\varepsilon _n)_n$
, we have  $$ \begin{align*} \frac{1}{2{\mathbf C}_{\ell}}\left\|\sum_{n\in A}e_n\right\|\ \leqslant\ \left\|\sum_{n\in A}\varepsilon_ne_n\right\| \ \leqslant\ 2{\mathbf C}_{\ell}\left\|\sum_{n\in A}e_n\right\|. \end{align*} $$
$$ \begin{align*} \frac{1}{2{\mathbf C}_{\ell}}\left\|\sum_{n\in A}e_n\right\|\ \leqslant\ \left\|\sum_{n\in A}\varepsilon_ne_n\right\| \ \leqslant\ 2{\mathbf C}_{\ell}\left\|\sum_{n\in A}e_n\right\|. \end{align*} $$
-
(2) For all
 $\alpha>0$
and
$\alpha>0$
and
 $x \in X$
, where
$x \in X$
, where $$ \begin{align*} \left\|\sum_{n \in \Gamma_{\alpha}(x)} \alpha \operatorname{\mathrm{sgn}}(e_n^*(x))e_n + \sum_{n \not \in \Gamma_{\alpha}(x)} e_n^*(x)e_n\right\|\ \leqslant\ \mathbf{C}_{\ell} \|x\|, \end{align*} $$
$$ \begin{align*} \left\|\sum_{n \in \Gamma_{\alpha}(x)} \alpha \operatorname{\mathrm{sgn}}(e_n^*(x))e_n + \sum_{n \not \in \Gamma_{\alpha}(x)} e_n^*(x)e_n\right\|\ \leqslant\ \mathbf{C}_{\ell} \|x\|, \end{align*} $$
 $\Gamma _{\alpha } (x) =\{n : |e^*_n(x)|>\alpha \}$
.
$\Gamma _{\alpha } (x) =\{n : |e^*_n(x)|>\alpha \}$
.
Proof of Proposition 2.5
It is obvious that Property (A,
![]() $\mathcal {F}$
) implies
$\mathcal {F}$
) implies
![]() $\mathcal {F}$
-disjoint democracy. Let us assume that
$\mathcal {F}$
-disjoint democracy. Let us assume that
![]() $(e_n)$
is
$(e_n)$
is
![]() ${\mathbf C}^{\mathcal {F}}_{d, \sqcup }$
-
${\mathbf C}^{\mathcal {F}}_{d, \sqcup }$
-
![]() $\mathcal {F}$
-disjoint democratic and is
$\mathcal {F}$
-disjoint democratic and is
![]() ${\mathbf C}_{\ell }$
-suppression quasi-greedy (or
${\mathbf C}_{\ell }$
-suppression quasi-greedy (or
![]() ${\mathbf C}_w$
-quasi-greedy). Let
${\mathbf C}_w$
-quasi-greedy). Let
![]() $x, A, B, (b_n), (\varepsilon _i)$
be as in Definition 2.1. Since B is a greedy set of
$x, A, B, (b_n), (\varepsilon _i)$
be as in Definition 2.1. Since B is a greedy set of
![]() $x+\sum _{n\in B}b_n e_n$
, we have
$x+\sum _{n\in B}b_n e_n$
, we have
 $$ \begin{align*} \left\|x+\sum_{n\in B}b_n e_n\right\|\ \geqslant\ \frac{1}{{\mathbf C}_w}\left\|\sum_{n\in B}b_n e_n\right\|&\ \geqslant\ \frac{1}{{\mathbf C}_w{\mathbf C}_{\ell}}\left\|\sum_{n\in B}\operatorname{\mathrm{sgn}}(b_n)e_n\right\|\mbox{ by Lemma}\ {2.6}\\ &\ \geqslant\ \frac{1}{2{\mathbf C}_w{\mathbf C}^2_{\ell}}\|1_B\|\mbox{ by Lemma}\ {2.6}\\ &\ \geqslant\ \frac{1}{2{\mathbf C}_w{\mathbf C}^2_{\ell}{\mathbf C}^{\mathcal{F}}_{d,\sqcup}}\|1_A\|\ \geqslant\ \frac{1}{4{\mathbf C}_w{\mathbf C}^3_{\ell}{\mathbf C}^{\mathcal{F}}_{d,\sqcup}}\|1_{\varepsilon A}\|. \end{align*} $$
$$ \begin{align*} \left\|x+\sum_{n\in B}b_n e_n\right\|\ \geqslant\ \frac{1}{{\mathbf C}_w}\left\|\sum_{n\in B}b_n e_n\right\|&\ \geqslant\ \frac{1}{{\mathbf C}_w{\mathbf C}_{\ell}}\left\|\sum_{n\in B}\operatorname{\mathrm{sgn}}(b_n)e_n\right\|\mbox{ by Lemma}\ {2.6}\\ &\ \geqslant\ \frac{1}{2{\mathbf C}_w{\mathbf C}^2_{\ell}}\|1_B\|\mbox{ by Lemma}\ {2.6}\\ &\ \geqslant\ \frac{1}{2{\mathbf C}_w{\mathbf C}^2_{\ell}{\mathbf C}^{\mathcal{F}}_{d,\sqcup}}\|1_A\|\ \geqslant\ \frac{1}{4{\mathbf C}_w{\mathbf C}^3_{\ell}{\mathbf C}^{\mathcal{F}}_{d,\sqcup}}\|1_{\varepsilon A}\|. \end{align*} $$
Again, since B is a greedy set of
![]() $x+\sum _{n\in B}b_n e_n$
,
$x+\sum _{n\in B}b_n e_n$
,
 $$ \begin{align*} \left\|x+\sum_{n\in B}b_n e_n\right\|\ \geqslant\ \frac{1}{{\mathbf C}_{\ell}}\|x\|. \end{align*} $$
$$ \begin{align*} \left\|x+\sum_{n\in B}b_n e_n\right\|\ \geqslant\ \frac{1}{{\mathbf C}_{\ell}}\|x\|. \end{align*} $$
Therefore, we obtain
 $$ \begin{align*}2\left\|x+\sum_{n\in B}b_n e_n\right\|\ \geqslant\ \frac{1}{4{\mathbf C}_w{\mathbf C}^3_{\ell}{\mathbf C}^{\mathcal{F}}_{d}}\|1_{\varepsilon A}\|+\frac{1}{{\mathbf C}_{\ell}}\|x\|\ \geqslant\ \frac{1}{4{\mathbf C}_w{\mathbf C}^3_{\ell}{\mathbf C}^{\mathcal{F}}_{d}}\|1_{\varepsilon A} + x\|.\end{align*} $$
$$ \begin{align*}2\left\|x+\sum_{n\in B}b_n e_n\right\|\ \geqslant\ \frac{1}{4{\mathbf C}_w{\mathbf C}^3_{\ell}{\mathbf C}^{\mathcal{F}}_{d}}\|1_{\varepsilon A}\|+\frac{1}{{\mathbf C}_{\ell}}\|x\|\ \geqslant\ \frac{1}{4{\mathbf C}_w{\mathbf C}^3_{\ell}{\mathbf C}^{\mathcal{F}}_{d}}\|1_{\varepsilon A} + x\|.\end{align*} $$
We have shown that
 $$ \begin{align*}\|x+ 1_{\varepsilon A}\|\ \leqslant\ 8{\mathbf C}_w{\mathbf C}^3_{\ell}{\mathbf C}^{\mathcal{F}}_{d}\left\|x+\sum_{n\in B}b_n e_n\right\|,\end{align*} $$
$$ \begin{align*}\|x+ 1_{\varepsilon A}\|\ \leqslant\ 8{\mathbf C}_w{\mathbf C}^3_{\ell}{\mathbf C}^{\mathcal{F}}_{d}\left\|x+\sum_{n\in B}b_n e_n\right\|,\end{align*} $$
which completes our proof that
![]() $(e_n)$
has Property (A,
$(e_n)$
has Property (A,
![]() $\mathcal {F}$
).
$\mathcal {F}$
).
Theorem 2.7 For a basis
![]() $(e_n)$
of a Banach space X, the following are equivalent:
$(e_n)$
of a Banach space X, the following are equivalent:
-
(1)
 $(e_n)$
is
$(e_n)$
is
 $\mathcal {F}$
-greedy.
$\mathcal {F}$
-greedy. -
(2)
 $(e_n)$
is
$(e_n)$
is
 $\mathcal {F}$
-unconditional and has Property (A,
$\mathcal {F}$
-unconditional and has Property (A,
 $\mathcal {F}$
).
$\mathcal {F}$
). -
(3)
 $(e_n)$
is
$(e_n)$
is
 $\mathcal {F}$
-unconditional,
$\mathcal {F}$
-unconditional,
 $\mathcal {F}$
-disjoint superdemocratic, and quasi-greedy.
$\mathcal {F}$
-disjoint superdemocratic, and quasi-greedy. -
(4)
 $(e_n)$
is
$(e_n)$
is
 $\mathcal {F}$
-unconditional,
$\mathcal {F}$
-unconditional,
 $\mathcal {F}$
-disjoint democratic, and quasi-greedy.
$\mathcal {F}$
-disjoint democratic, and quasi-greedy.
Proof of Theorem 2.7
By Theorem 2.3, we have that (1)
![]() $\Longleftrightarrow $
(2). Since an
$\Longleftrightarrow $
(2). Since an
![]() $\mathcal {F}$
-greedy basis is quasi-greedy, and Property (A,
$\mathcal {F}$
-greedy basis is quasi-greedy, and Property (A,
![]() $\mathcal {F}$
) implies
$\mathcal {F}$
) implies
![]() $\mathcal {F}$
-disjoint superdemocracy (by definition), we get (1)
$\mathcal {F}$
-disjoint superdemocracy (by definition), we get (1)
![]() $\Longleftrightarrow $
(2)
$\Longleftrightarrow $
(2)
![]() $\Longrightarrow $
(3). Trivially, (3)
$\Longrightarrow $
(3). Trivially, (3)
![]() $\Longrightarrow $
(4). That (4)
$\Longrightarrow $
(4). That (4)
![]() $\Longrightarrow $
(2) is due to Proposition 2.5.
$\Longrightarrow $
(2) is due to Proposition 2.5.
3 Characterizations of
 $\mathcal {F}$
-almost greedy bases
$\mathcal {F}$
-almost greedy bases
In this section, we first characterize
![]() $\mathcal {F}$
-almost greedy bases using Property (A,
$\mathcal {F}$
-almost greedy bases using Property (A,
![]() $\mathcal {F}$
), then show that the
$\mathcal {F}$
), then show that the
![]() $\mathcal {F}$
-almost greedy property is equivalent to the quasi-greedy property plus
$\mathcal {F}$
-almost greedy property is equivalent to the quasi-greedy property plus
![]() $\mathcal {F}$
-disjoint superdemocracy.
$\mathcal {F}$
-disjoint superdemocracy.
Theorem 3.1 A basis
![]() $(e_n)$
is C-
$(e_n)$
is C-
![]() $\mathcal {F}$
-almost greedy if and only if
$\mathcal {F}$
-almost greedy if and only if
![]() $(e_n)$
has C-Property (A,
$(e_n)$
has C-Property (A,
![]() $\mathcal {F}$
).
$\mathcal {F}$
).
Proof of Theorem 3.1
The proof that C-
![]() $\mathcal {F}$
-almost greediness implies that C-Property (A,
$\mathcal {F}$
-almost greediness implies that C-Property (A,
![]() $\mathcal {F}$
) is similar to what we have in the proof of Theorem 2.3. Conversely, assume that
$\mathcal {F}$
) is similar to what we have in the proof of Theorem 2.3. Conversely, assume that
![]() $(e_n)$
has C-Property (A,
$(e_n)$
has C-Property (A,
![]() $\mathcal {F}$
). Let
$\mathcal {F}$
). Let
![]() $x\in \mathbb {X}$
with a greedy set A. Choose
$x\in \mathbb {X}$
with a greedy set A. Choose
![]() $B\in \mathcal {F}$
with
$B\in \mathcal {F}$
with
![]() $|B|\leqslant |A|$
. If
$|B|\leqslant |A|$
. If
![]() $A\backslash B = \emptyset $
, then
$A\backslash B = \emptyset $
, then
![]() $A = B$
and
$A = B$
and
![]() $\|x-P_A(x)\| = \|x-P_B(x)\|$
. If
$\|x-P_A(x)\| = \|x-P_B(x)\|$
. If
![]() $A\backslash B\neq \emptyset $
, note that
$A\backslash B\neq \emptyset $
, note that
![]() $\min _{n\in A\backslash B}|e_n^*(x)|\geqslant \|x-P_A(x)\|_{\infty }$
. By Proposition 2.2, we have
$\min _{n\in A\backslash B}|e_n^*(x)|\geqslant \|x-P_A(x)\|_{\infty }$
. By Proposition 2.2, we have
 $$ \begin{align*} \|x-P_A(x)\|&\ \leqslant\ C\|(x-P_A(x)) - P_{B\backslash A}(x) + P_{A\backslash B}(x)\|\\ &\ =\ C\|x-P_B(x)\|. \end{align*} $$
$$ \begin{align*} \|x-P_A(x)\|&\ \leqslant\ C\|(x-P_A(x)) - P_{B\backslash A}(x) + P_{A\backslash B}(x)\|\\ &\ =\ C\|x-P_B(x)\|. \end{align*} $$
Since B is arbitrary, we know that
![]() $(e_n)$
is C-
$(e_n)$
is C-
![]() $\mathcal {F}$
-almost greedy.
$\mathcal {F}$
-almost greedy.
Theorem 3.2 Let
![]() $(e_n)$
be a basis. The following are equivalent:
$(e_n)$
be a basis. The following are equivalent:
-
(1)
 $(e_n)$
is
$(e_n)$
is
 $\mathcal {F}$
-almost greedy.
$\mathcal {F}$
-almost greedy. -
(2)
 $(e_n)$
has Property (A,
$(e_n)$
has Property (A,
 $\mathcal {F}$
).
$\mathcal {F}$
). -
(3)
 $(e_n)$
is
$(e_n)$
is
 $\mathcal {F}$
-disjoint superdemocratic and quasi-greedy.
$\mathcal {F}$
-disjoint superdemocratic and quasi-greedy. -
(4)
 $(e_n)$
is
$(e_n)$
is
 $\mathcal {F}$
-disjoint democratic and quasi-greedy.
$\mathcal {F}$
-disjoint democratic and quasi-greedy.
Proof of Theorem 3.2
That (1)
![]() $\Longleftrightarrow $
(2) follows from Theorem 3.1. Clearly, an
$\Longleftrightarrow $
(2) follows from Theorem 3.1. Clearly, an
![]() $\mathcal {F}$
-almost greedy basis is quasi-greedy. By Proposition 2.5, we have (2)
$\mathcal {F}$
-almost greedy basis is quasi-greedy. By Proposition 2.5, we have (2)
![]() $\Longleftrightarrow $
(4). Since (1)
$\Longleftrightarrow $
(4). Since (1)
![]() $\Longleftrightarrow $
(2)
$\Longleftrightarrow $
(2)
![]() $\Longrightarrow $
(3)
$\Longrightarrow $
(3)
![]() $\Longrightarrow $
(4), we are done.
$\Longrightarrow $
(4), we are done.
Corollary 3.3 (Generalization of Theorem 2.3 in [Reference Albiac and Ansorena1])
A basis
![]() $(e_n)$
is
$(e_n)$
is
![]() $1$
-
$1$
-
![]() $\mathcal {F}$
-almost greedy if and only if
$\mathcal {F}$
-almost greedy if and only if
![]() $(e_n)$
has
$(e_n)$
has
![]() $1$
-Property (A,
$1$
-Property (A,
![]() $\mathcal {F}$
).
$\mathcal {F}$
).
4 Schreier families and
 $\mathcal {S}_{\alpha }$
-greedy bases
$\mathcal {S}_{\alpha }$
-greedy bases
In this section, we will provide several nontrivial examples of
![]() $\mathcal {F}$
-greedy basis. In particular, we will consider bases that are quasi-greedy but not greedy. As mentioned in the introduction, the Schreier families
$\mathcal {F}$
-greedy basis. In particular, we will consider bases that are quasi-greedy but not greedy. As mentioned in the introduction, the Schreier families
![]() $\mathcal {S}_{\alpha }$
form a particularly rich collection of finite subsets of
$\mathcal {S}_{\alpha }$
form a particularly rich collection of finite subsets of
![]() $\mathbb {N}$
.
$\mathbb {N}$
.
Proof of Corollary 1.9
Fix two countable ordinals
![]() $\alpha < \beta $
. Let N be as in Proposition 1.8. Suppose that
$\alpha < \beta $
. Let N be as in Proposition 1.8. Suppose that
![]() $(e_n)$
is C-
$(e_n)$
is C-
![]() $\mathcal {S}_{\beta }$
-greedy for some constant
$\mathcal {S}_{\beta }$
-greedy for some constant
![]() $C\geqslant 1$
. By Theorems 1.5 and 2.3,
$C\geqslant 1$
. By Theorems 1.5 and 2.3,
![]() $(e_n)$
is C-
$(e_n)$
is C-
![]() $\mathcal {S}_{\beta }$
-suppression unconditional, C-
$\mathcal {S}_{\beta }$
-suppression unconditional, C-
![]() $\mathcal {S}_{\beta }$
-disjoint democratic, and C-suppression quasi-greedy.
$\mathcal {S}_{\beta }$
-disjoint democratic, and C-suppression quasi-greedy.
We show that
![]() $(e_n)$
is C-
$(e_n)$
is C-
![]() $\mathcal {S}_{\alpha }$
-suppression unconditional. Let
$\mathcal {S}_{\alpha }$
-suppression unconditional. Let
![]() $x\in X$
and
$x\in X$
and
![]() $E\in \mathcal {S}_{\alpha }$
. We know that
$E\in \mathcal {S}_{\alpha }$
. We know that
![]() $E\backslash \{1, \ldots , N-1\}\in \mathcal {S}_{\beta }$
. Hence,
$E\backslash \{1, \ldots , N-1\}\in \mathcal {S}_{\beta }$
. Hence,
We have
 $$ \begin{align*} \|x-P_{E}(x)\|&\ \leqslant\ \|x-P_{E\backslash \{1, \ldots, N-1\}}(x)\| + \|P_{E\cap \{1, \ldots, N-1\}}(x)\|\\ &\ \leqslant\ C\|x\| + N\sup_{n}\|e_n\|\|e_n^*\|\|x\|\ \leqslant\ (C+Nc_2^2)\|x\|. \end{align*} $$
$$ \begin{align*} \|x-P_{E}(x)\|&\ \leqslant\ \|x-P_{E\backslash \{1, \ldots, N-1\}}(x)\| + \|P_{E\cap \{1, \ldots, N-1\}}(x)\|\\ &\ \leqslant\ C\|x\| + N\sup_{n}\|e_n\|\|e_n^*\|\|x\|\ \leqslant\ (C+Nc_2^2)\|x\|. \end{align*} $$
Therefore,
![]() $(e_n)$
is
$(e_n)$
is
![]() $\mathcal {S}_{\alpha }$
-suppression unconditional.
$\mathcal {S}_{\alpha }$
-suppression unconditional.
Next, we show that
![]() $(e_n)$
is C-
$(e_n)$
is C-
![]() $\mathcal {S}_{\alpha }$
-disjoint democratic. Let
$\mathcal {S}_{\alpha }$
-disjoint democratic. Let
![]() $A\in \mathcal {S}_{\alpha }$
and
$A\in \mathcal {S}_{\alpha }$
and
![]() $B\subset \mathbb {N}$
such that
$B\subset \mathbb {N}$
such that
![]() $A\cap B = \emptyset $
and
$A\cap B = \emptyset $
and
![]() $|A|\leqslant |B|$
. Since
$|A|\leqslant |B|$
. Since
![]() $A\backslash \{1, \ldots , N-1\}\in \mathcal {S}_{\beta }$
, we have
$A\backslash \{1, \ldots , N-1\}\in \mathcal {S}_{\beta }$
, we have
Also, due to C-quasi-greediness,
Hence,
 $$ \begin{align*} \|1_A\|&\ \leqslant\ \|1_{A\backslash \{1, \ldots, N-1\}}\| + \|1_{A\cap \{1, \ldots, N-1\}}\|\\ &\ \leqslant\ C\|1_B\| + c_2N\ \leqslant\ C\|1_B\| + \frac{Cc_2N}{c_1}\|1_B\|\ =\ C\left(1+N\frac{c_2}{c_1}\right)\|1_B\|. \end{align*} $$
$$ \begin{align*} \|1_A\|&\ \leqslant\ \|1_{A\backslash \{1, \ldots, N-1\}}\| + \|1_{A\cap \{1, \ldots, N-1\}}\|\\ &\ \leqslant\ C\|1_B\| + c_2N\ \leqslant\ C\|1_B\| + \frac{Cc_2N}{c_1}\|1_B\|\ =\ C\left(1+N\frac{c_2}{c_1}\right)\|1_B\|. \end{align*} $$
Therefore,
![]() $(e_n)$
is
$(e_n)$
is
![]() $\mathcal {S}_{\alpha }$
-disjoint democratic.
$\mathcal {S}_{\alpha }$
-disjoint democratic.
By Theorem 1.5, we conclude that
![]() $(e_n)$
is
$(e_n)$
is
![]() $\mathcal {S}_{\alpha }$
-greedy.
$\mathcal {S}_{\alpha }$
-greedy.
We have
We construct bases to show that none of the reverse implications holds. Consider the following definition.
Definition 4.1 Let
![]() $\omega _1$
denote the set of all countable ordinals and
$\omega _1$
denote the set of all countable ordinals and
![]() $(\alpha ,\beta ) \in (\omega _1\cup \{\infty \})^2$
. A quasi-greedy basis
$(\alpha ,\beta ) \in (\omega _1\cup \{\infty \})^2$
. A quasi-greedy basis
![]() $(e_n)$
for a Banach space X is called
$(e_n)$
for a Banach space X is called
![]() $(\alpha ,\beta )$
-quasi-greedy if and only if
$(\alpha ,\beta )$
-quasi-greedy if and only if
![]() $(e_n)$
is
$(e_n)$
is
![]() $\mathcal {S}_{\alpha }$
-unconditional but not
$\mathcal {S}_{\alpha }$
-unconditional but not
![]() $\mathcal {S}_{\alpha +1}$
-unconditional and
$\mathcal {S}_{\alpha +1}$
-unconditional and
![]() $\mathcal {S}_{\beta }$
-disjoint democratic but not
$\mathcal {S}_{\beta }$
-disjoint democratic but not
![]() $\mathcal {S}_{\beta +1}$
-disjoint democratic.
$\mathcal {S}_{\beta +1}$
-disjoint democratic.
Suppose that either
![]() $\alpha $
or
$\alpha $
or
![]() $\beta $
is
$\beta $
is
![]() $\infty $
. If we denote by
$\infty $
. If we denote by
![]() $\mathcal {S}_{\infty }$
the set of all finite subsets of
$\mathcal {S}_{\infty }$
the set of all finite subsets of
![]() $\mathbb {N}$
, then
$\mathbb {N}$
, then
![]() $\mathcal {S}_{\infty }$
-unconditionality and
$\mathcal {S}_{\infty }$
-unconditionality and
![]() $\mathcal {S}_{\infty }$
-disjoint democracy coincide with unconditionality and disjoint democracy, respectively.
$\mathcal {S}_{\infty }$
-disjoint democracy coincide with unconditionality and disjoint democracy, respectively.
Remark 4.2 Due to the proof of Corollary 1.9, a basis
![]() $(e_n)$
for a Banach space X is
$(e_n)$
for a Banach space X is
![]() $\mathcal {S}_{\eta }$
-greedy if and only if it is
$\mathcal {S}_{\eta }$
-greedy if and only if it is
![]() $(\alpha ,\beta )$
-quasi-greedy for some
$(\alpha ,\beta )$
-quasi-greedy for some
![]() $\alpha \geqslant \eta $
and
$\alpha \geqslant \eta $
and
![]() $\beta \geqslant \eta $
. Note also that the
$\beta \geqslant \eta $
. Note also that the
![]() $(\infty ,\infty )$
-quasi-greedy property is the same as the greedy property, and a
$(\infty ,\infty )$
-quasi-greedy property is the same as the greedy property, and a
![]() $(0,0)$
-quasi-greedy basis is quasi-greedy but is far from being greedy.
$(0,0)$
-quasi-greedy basis is quasi-greedy but is far from being greedy.
We prove Theorem 1.10 by providing the following examples.
Theorem 4.3 There are spaces with bases
![]() $(e_n)$
that are
$(e_n)$
that are
![]() $(0,0)$
-quasi-greedy,
$(0,0)$
-quasi-greedy,
![]() $(\infty , 0)$
-quasi-greedy, and
$(\infty , 0)$
-quasi-greedy, and
![]() $(0, \infty )$
-quasi-greedy.
$(0, \infty )$
-quasi-greedy.
Theorem 4.4 Fix a nonzero
![]() $\alpha \in \omega _1$
. There is a space
$\alpha \in \omega _1$
. There is a space
![]() $X_{\alpha ,\infty }$
with a basis
$X_{\alpha ,\infty }$
with a basis
![]() $(e_n)$
that is
$(e_n)$
that is
![]() $(\alpha ,\infty )$
-quasi-greedy. Hence,
$(\alpha ,\infty )$
-quasi-greedy. Hence,
![]() $X_{\alpha ,\infty }$
is
$X_{\alpha ,\infty }$
is
![]() $\mathcal {S}_{\alpha }$
-greedy but not
$\mathcal {S}_{\alpha }$
-greedy but not
![]() $\mathcal {S}_{\alpha +1}$
-greedy.
$\mathcal {S}_{\alpha +1}$
-greedy.
Theorem 4.5 Fix a nonzero
![]() $\alpha \in \omega _1$
. There is a space
$\alpha \in \omega _1$
. There is a space
![]() $X_{\infty , \alpha }$
with a basis
$X_{\infty , \alpha }$
with a basis
![]() $(e_n)$
that is
$(e_n)$
that is
![]() $(\infty , \alpha )$
-quasi-greedy. Hence,
$(\infty , \alpha )$
-quasi-greedy. Hence,
![]() $X_{\infty , \alpha }$
is
$X_{\infty , \alpha }$
is
![]() $\mathcal {S}_{\alpha }$
-greedy but not
$\mathcal {S}_{\alpha }$
-greedy but not
![]() $\mathcal {S}_{\alpha +1}$
-greedy.
$\mathcal {S}_{\alpha +1}$
-greedy.
Remark 4.6 The bases we construct in Theorem 4.4 give new examples of conditional quasi-greedy bases. Furthermore, these bases are
![]() $1$
-suppression quasi-greedy.
$1$
-suppression quasi-greedy.
4.1 Proof of Theorem 4.3
4.1.1 A
 $(0,0)$
-quasi-greedy basis
$(0,0)$
-quasi-greedy basis
We modify an example by Konyagin and Temlyakov [Reference Konyagin and Temlyakov15] who gave a conditional basis that is quasi-greedy. We shall construct a quasi-greedy basis that is neither
![]() $\mathcal {S}_1$
-disjoint democratic nor
$\mathcal {S}_1$
-disjoint democratic nor
![]() $\mathcal {S}_1$
-unconditional. For each
$\mathcal {S}_1$
-unconditional. For each
![]() $N\in \mathbb {N}$
, let
$N\in \mathbb {N}$
, let
![]() $X_N$
be the
$X_N$
be the
![]() $(2N-1)$
-dimensional space that is the completion of
$(2N-1)$
-dimensional space that is the completion of
![]() $c_{00}$
under the norm: for
$c_{00}$
under the norm: for
![]() $x = (a_i)_i$
,
$x = (a_i)_i$
,
 $$ \begin{align*} \|(a_i)_i\|\ =\ \max\left\{\left(\sum_{i=1}^{2N-1}|a_i|^2\right)^{1/2}, \sup_{N\leqslant m\leqslant 2N-1}\left|\sum_{i=N}^m \frac{1}{\sqrt{i-N+1}}a_i\right|\right\}. \end{align*} $$
$$ \begin{align*} \|(a_i)_i\|\ =\ \max\left\{\left(\sum_{i=1}^{2N-1}|a_i|^2\right)^{1/2}, \sup_{N\leqslant m\leqslant 2N-1}\left|\sum_{i=N}^m \frac{1}{\sqrt{i-N+1}}a_i\right|\right\}. \end{align*} $$
Let
![]() $X = (\oplus _{N=1}^{\infty } X_N)_{c_0}$
. Let
$X = (\oplus _{N=1}^{\infty } X_N)_{c_0}$
. Let
![]() $\mathcal {B}$
be the canonical basis of X.
$\mathcal {B}$
be the canonical basis of X.
Theorem 4.7 The basis
![]() $\mathcal {B}$
is
$\mathcal {B}$
is
![]() $(0,0)$
-quasi-greedy.
$(0,0)$
-quasi-greedy.
Proof First, we show that
![]() $\mathcal {B}$
is not
$\mathcal {B}$
is not
![]() $\mathcal {S}_1$
-unconditional. For each
$\mathcal {S}_1$
-unconditional. For each
![]() $X_N$
, let
$X_N$
, let
![]() $(f^N_i)_{i=1}^{2N-1}$
be the canonical basis of
$(f^N_i)_{i=1}^{2N-1}$
be the canonical basis of
![]() $X_N$
(that also belongs to
$X_N$
(that also belongs to
![]() $\mathcal {B}$
). We have
$\mathcal {B}$
). We have
 $$ \begin{align*} \left\|\sum_{i=N}^{2N-1}\frac{1}{\sqrt{i-N+1}}f^N_i\right\|\ =\ \sum_{i=1}^N\frac{1}{i},\mbox{ while } \left\|\sum_{i=N}^{2N-1}\frac{(-1)^i}{\sqrt{i-N+1}}f^N_i\right\|\ =\ \left(\sum_{i=1}^N\frac{1}{i}\right)^{1/2}. \end{align*} $$
$$ \begin{align*} \left\|\sum_{i=N}^{2N-1}\frac{1}{\sqrt{i-N+1}}f^N_i\right\|\ =\ \sum_{i=1}^N\frac{1}{i},\mbox{ while } \left\|\sum_{i=N}^{2N-1}\frac{(-1)^i}{\sqrt{i-N+1}}f^N_i\right\|\ =\ \left(\sum_{i=1}^N\frac{1}{i}\right)^{1/2}. \end{align*} $$
As
![]() $N\rightarrow \infty $
,
$N\rightarrow \infty $
,
![]() $\left \|\sum _{i=N}^{2N-1}\frac {1}{\sqrt {i-N+1}}f^N_i\right \|/\left \|\sum _{i=N}^{2N-1}\frac {(-1)^i}{\sqrt {i-N+1}}f^N_i\right \|\rightarrow \infty $
; hence,
$\left \|\sum _{i=N}^{2N-1}\frac {1}{\sqrt {i-N+1}}f^N_i\right \|/\left \|\sum _{i=N}^{2N-1}\frac {(-1)^i}{\sqrt {i-N+1}}f^N_i\right \|\rightarrow \infty $
; hence,
![]() $\mathcal {B}$
is not
$\mathcal {B}$
is not
![]() $\mathcal {S}_1$
-unconditional.
$\mathcal {S}_1$
-unconditional.
Next, we show that
![]() $\mathcal {B}$
is not
$\mathcal {B}$
is not
![]() $\mathcal {S}_1$
-disjoint democratic. We have
$\mathcal {S}_1$
-disjoint democratic. We have
 $$ \begin{align*} \left\|\sum_{i=N}^{2N-1}f^N_i\right\|\ =\ \sum_{i=1}^{N}\frac{1}{\sqrt{i}}, \mbox{ while }\left\|\sum_{i=N+1}^{2N} f^i_1\right\|\ =\ 1.\end{align*} $$
$$ \begin{align*} \left\|\sum_{i=N}^{2N-1}f^N_i\right\|\ =\ \sum_{i=1}^{N}\frac{1}{\sqrt{i}}, \mbox{ while }\left\|\sum_{i=N+1}^{2N} f^i_1\right\|\ =\ 1.\end{align*} $$
Therefore,
![]() $\mathcal {B}$
is not
$\mathcal {B}$
is not
![]() $\mathcal {S}_1$
-disjoint democratic.
$\mathcal {S}_1$
-disjoint democratic.
Finally, we prove that
![]() $\mathcal {B}$
is quasi-greedy. To do so, we need only to show that for each N, the basis
$\mathcal {B}$
is quasi-greedy. To do so, we need only to show that for each N, the basis
![]() $(f^N_i)_{i=1}^{2N-1}$
has the same quasi-greedy constant of
$(f^N_i)_{i=1}^{2N-1}$
has the same quasi-greedy constant of
![]() $3 + \sqrt {2}$
. Let
$3 + \sqrt {2}$
. Let
![]() ${(a_i)_{i=1}^{2N-1}\in X_N}$
, where
${(a_i)_{i=1}^{2N-1}\in X_N}$
, where
![]() $\|(a_i)_i\|\leqslant 1$
. It suffices to prove that
$\|(a_i)_i\|\leqslant 1$
. It suffices to prove that
 $$ \begin{align*} \left|\sum_{i\in \Lambda}\frac{1}{\sqrt{i-N+1}}a_i\right|\ \leqslant\ 3+\sqrt{2}, \end{align*} $$
$$ \begin{align*} \left|\sum_{i\in \Lambda}\frac{1}{\sqrt{i-N+1}}a_i\right|\ \leqslant\ 3+\sqrt{2}, \end{align*} $$
for all
![]() $\varepsilon> 0$
, for all
$\varepsilon> 0$
, for all
![]() $M\in [N, 2N-1]$
, and for
$M\in [N, 2N-1]$
, and for
![]() $\Lambda = \{N\leqslant i\leqslant M: |a_i|>\varepsilon \}$
. Since
$\Lambda = \{N\leqslant i\leqslant M: |a_i|>\varepsilon \}$
. Since
![]() $\|(a_i)_i\|\leqslant 1$
, we know that
$\|(a_i)_i\|\leqslant 1$
, we know that
![]() $|a_i|\leqslant 1$
, and so we can assume that
$|a_i|\leqslant 1$
, and so we can assume that
![]() $0 < \varepsilon < 1$
. Set
$0 < \varepsilon < 1$
. Set
![]() $L = \lfloor \varepsilon ^{-2}\rfloor $
to have
$L = \lfloor \varepsilon ^{-2}\rfloor $
to have
![]() $1/2 \leqslant \varepsilon ^2 L\leqslant 1$
. We proceed by case analysis.
$1/2 \leqslant \varepsilon ^2 L\leqslant 1$
. We proceed by case analysis.
Case 1:
![]() $M-N+1\leqslant L$
. We have
$M-N+1\leqslant L$
. We have
 $$ \begin{align*} \left|\sum_{i\in \Lambda}\frac{a_i}{\sqrt{i-N+1}}\right|&\ \leqslant\ \left|\sum_{N\leqslant i\leqslant M}\frac{a_i}{\sqrt{i-N+1}}\right| + \left|\sum_{\substack{N\leqslant i\leqslant M\\|a_i| \leqslant \varepsilon}}\frac{a_i}{\sqrt{i-N+1}}\right|\\ &\ \leqslant\ 1 + \varepsilon \sum_{i=N}^{M}\frac{1}{\sqrt{i-N+1}}\\ &\ \leqslant\ 1 + \varepsilon \sum_{i=1}^{M-N+1}\frac{1}{\sqrt{i}}\\ &\ \leqslant\ 1 + 2\varepsilon\sqrt{M-N+1}\ \leqslant\ 1 + 2\varepsilon \sqrt{L}\ \leqslant\ 3. \end{align*} $$
$$ \begin{align*} \left|\sum_{i\in \Lambda}\frac{a_i}{\sqrt{i-N+1}}\right|&\ \leqslant\ \left|\sum_{N\leqslant i\leqslant M}\frac{a_i}{\sqrt{i-N+1}}\right| + \left|\sum_{\substack{N\leqslant i\leqslant M\\|a_i| \leqslant \varepsilon}}\frac{a_i}{\sqrt{i-N+1}}\right|\\ &\ \leqslant\ 1 + \varepsilon \sum_{i=N}^{M}\frac{1}{\sqrt{i-N+1}}\\ &\ \leqslant\ 1 + \varepsilon \sum_{i=1}^{M-N+1}\frac{1}{\sqrt{i}}\\ &\ \leqslant\ 1 + 2\varepsilon\sqrt{M-N+1}\ \leqslant\ 1 + 2\varepsilon \sqrt{L}\ \leqslant\ 3. \end{align*} $$
Case 2:
![]() $M-N+1> L$
. We have
$M-N+1> L$
. We have
 $$ \begin{align*} \left|\sum_{i\in \Lambda}\frac{a_i}{\sqrt{i-N+1}}\right|\ =\ \left|\sum_{\substack{N\leqslant i\leqslant N+L-1\\ |a_i|> \varepsilon}}\frac{a_i}{\sqrt{i-N+1}}\right| + \left|\sum_{\substack{N+L\leqslant i\leqslant M\\|a_i| > \varepsilon}}\frac{a_i}{\sqrt{i-N+1}}\right|. \end{align*} $$
$$ \begin{align*} \left|\sum_{i\in \Lambda}\frac{a_i}{\sqrt{i-N+1}}\right|\ =\ \left|\sum_{\substack{N\leqslant i\leqslant N+L-1\\ |a_i|> \varepsilon}}\frac{a_i}{\sqrt{i-N+1}}\right| + \left|\sum_{\substack{N+L\leqslant i\leqslant M\\|a_i| > \varepsilon}}\frac{a_i}{\sqrt{i-N+1}}\right|. \end{align*} $$
By above,
 $$ \begin{align*}\left|\sum_{\substack{N\leqslant i\leqslant N+L-1\\ |a_i|> \varepsilon}}\frac{a_i}{\sqrt{i-N+1}}\right|\ \leqslant\ 3.\end{align*} $$
$$ \begin{align*}\left|\sum_{\substack{N\leqslant i\leqslant N+L-1\\ |a_i|> \varepsilon}}\frac{a_i}{\sqrt{i-N+1}}\right|\ \leqslant\ 3.\end{align*} $$
Furthermore, we have
 $$ \begin{align*} \left|\sum_{\substack{N+L\leqslant i\leqslant M\\ |a_i|> \varepsilon}}\frac{a_i}{\sqrt{i-N+1}}\right| &\ \leqslant\ \left(\sum_{N+L\leqslant i\leqslant M}\frac{1}{(i-N+1)^{3/2}}\right)^{1/3}\left(\sum_{\substack{N+L\leqslant i\leqslant M\\|a_i|>\varepsilon}}|a_i|^{3/2}\right)^{2/3}\\ &\ \leqslant\ \left(\sum_{i=L+1}^{\infty} \frac{1}{i^{3/2}}\right)^{1/3}\left(\sum_{\substack{N+L\leqslant i\leqslant M\\|a_i| > \varepsilon}}|a_i|^{3/2}\sqrt{\frac{|a_i|}{\varepsilon}}\right)^{2/3}\\ &\ \leqslant\ 2^{1/3}L^{-1/6}\varepsilon^{-1/3}\ \leqslant \ \sqrt{2}. \end{align*} $$
$$ \begin{align*} \left|\sum_{\substack{N+L\leqslant i\leqslant M\\ |a_i|> \varepsilon}}\frac{a_i}{\sqrt{i-N+1}}\right| &\ \leqslant\ \left(\sum_{N+L\leqslant i\leqslant M}\frac{1}{(i-N+1)^{3/2}}\right)^{1/3}\left(\sum_{\substack{N+L\leqslant i\leqslant M\\|a_i|>\varepsilon}}|a_i|^{3/2}\right)^{2/3}\\ &\ \leqslant\ \left(\sum_{i=L+1}^{\infty} \frac{1}{i^{3/2}}\right)^{1/3}\left(\sum_{\substack{N+L\leqslant i\leqslant M\\|a_i| > \varepsilon}}|a_i|^{3/2}\sqrt{\frac{|a_i|}{\varepsilon}}\right)^{2/3}\\ &\ \leqslant\ 2^{1/3}L^{-1/6}\varepsilon^{-1/3}\ \leqslant \ \sqrt{2}. \end{align*} $$
This completes our proof.
4.1.2 An
 $(\infty , 0)$
-quasi-greedy basis
$(\infty , 0)$
-quasi-greedy basis
Define
Let
![]() $\mathbb {X}$
be the completion of
$\mathbb {X}$
be the completion of
![]() $c_{00}$
with respect to the following norm: for
$c_{00}$
with respect to the following norm: for
![]() $x = (x_1, x_2, \ldots )$
, let
$x = (x_1, x_2, \ldots )$
, let
 $$ \begin{align*} \|x\|\ :=\ \left(\sum_{2|i}|x_i|\right) + \left(\sum_{2\nmid i}|x_i|^2\right)^{1/2}. \end{align*} $$
$$ \begin{align*} \|x\|\ :=\ \left(\sum_{2|i}|x_i|\right) + \left(\sum_{2\nmid i}|x_i|^2\right)^{1/2}. \end{align*} $$
Let
![]() $\mathcal {B}$
be the canonical basis. Clearly,
$\mathcal {B}$
be the canonical basis. Clearly,
![]() $\mathcal {B}$
is
$\mathcal {B}$
is
![]() $1$
-unconditional. Note that
$1$
-unconditional. Note that
![]() $\mathcal {B}$
is not
$\mathcal {B}$
is not
![]() $\mathcal {S}_1$
-disjoint democratic. To see this, fix
$\mathcal {S}_1$
-disjoint democratic. To see this, fix
![]() $N\in \mathbb {N}$
and choose
$N\in \mathbb {N}$
and choose
![]() $A = \{1, 3, 5, \ldots , 2N-1\}$
and
$A = \{1, 3, 5, \ldots , 2N-1\}$
and
![]() $B = \{2N, 2N+2, 2N+4, \ldots , 4N-2\}\in \mathcal {S}_1$
. Then
$B = \{2N, 2N+2, 2N+4, \ldots , 4N-2\}\in \mathcal {S}_1$
. Then
![]() $\|1_A\| = \sqrt {N}$
, while
$\|1_A\| = \sqrt {N}$
, while
![]() $\|1_B\| = N$
. Hence,
$\|1_B\| = N$
. Hence,
![]() $\|1_B\|/\|1_A\|\rightarrow \infty $
as
$\|1_B\|/\|1_A\|\rightarrow \infty $
as
![]() $N\rightarrow \infty $
. It follows that
$N\rightarrow \infty $
. It follows that
![]() $\mathcal {B}$
is not
$\mathcal {B}$
is not
![]() $\mathcal {S}_1$
-disjoint democratic.
$\mathcal {S}_1$
-disjoint democratic.
4.1.3 A
 $(0,\infty )$
-quasi-greedy basis
$(0,\infty )$
-quasi-greedy basis
We define the spaces
![]() $X_N$
as in Section 4.1.1: for each
$X_N$
as in Section 4.1.1: for each
![]() $N\in \mathbb {N}$
, let
$N\in \mathbb {N}$
, let
![]() $X_N$
be the
$X_N$
be the
![]() $(2N-1)$
-dimensional space that is the completion of
$(2N-1)$
-dimensional space that is the completion of
![]() $c_{00}$
under the norm: for
$c_{00}$
under the norm: for
![]() $x = (a_i)_i$
,
$x = (a_i)_i$
,
 $$ \begin{align*} \|(a_i)_i\|\ =\ \max\left\{\left(\sum_{i=1}^{2N-1}|a_i|^2\right)^{1/2}, \sup_{N\leqslant m\leqslant 2N-1}\left|\sum_{i=N}^m \frac{1}{\sqrt{i-N+1}}a_i\right|\right\}. \end{align*} $$
$$ \begin{align*} \|(a_i)_i\|\ =\ \max\left\{\left(\sum_{i=1}^{2N-1}|a_i|^2\right)^{1/2}, \sup_{N\leqslant m\leqslant 2N-1}\left|\sum_{i=N}^m \frac{1}{\sqrt{i-N+1}}a_i\right|\right\}. \end{align*} $$
Let
![]() $X = (\oplus _{N=1}^{\infty } X_N)_{\ell _2}$
. Let
$X = (\oplus _{N=1}^{\infty } X_N)_{\ell _2}$
. Let
![]() $\mathcal {B}$
be the canonical basis of X. Using the same argument as in Section 4.1, we know that
$\mathcal {B}$
be the canonical basis of X. Using the same argument as in Section 4.1, we know that
![]() $\mathcal {B}$
is quasi-greedy and is not
$\mathcal {B}$
is quasi-greedy and is not
![]() $\mathcal {S}_1$
-unconditional. We show that
$\mathcal {S}_1$
-unconditional. We show that
![]() $\mathcal {B}$
is democratic. Let
$\mathcal {B}$
is democratic. Let
![]() $A\subset \mathcal {B}$
be a nonempty finite set. Write
$A\subset \mathcal {B}$
be a nonempty finite set. Write
![]() $A = \bigcup _{N=1}^{\infty } A_N$
, where
$A = \bigcup _{N=1}^{\infty } A_N$
, where
![]() $A_N$
is the intersection of A and the canonical basis of
$A_N$
is the intersection of A and the canonical basis of
![]() $X_N$
. We have
$X_N$
. We have
 $$ \begin{align*} \left\|\sum_{e\in A} e\right\|\ =\ \left(\sum_{N=1}^{\infty}\left\|\sum_{e\in A_N} e\right\|^2\right)^{1/2}\ \geqslant\ \left(\sum_{N=1}^{\infty}|A_N|\right)^{1/2}\ =\ |A|^{1/2}. \end{align*} $$
$$ \begin{align*} \left\|\sum_{e\in A} e\right\|\ =\ \left(\sum_{N=1}^{\infty}\left\|\sum_{e\in A_N} e\right\|^2\right)^{1/2}\ \geqslant\ \left(\sum_{N=1}^{\infty}|A_N|\right)^{1/2}\ =\ |A|^{1/2}. \end{align*} $$
On the other hand, for each N,
 $$ \begin{align*} \left\|\sum_{e\in A_N}e\right\|\ \leqslant\ \sum_{i=1}^{|A_N|}\frac{1}{\sqrt{i}}\ \leqslant\ 2\sqrt{|A_N|}. \end{align*} $$
$$ \begin{align*} \left\|\sum_{e\in A_N}e\right\|\ \leqslant\ \sum_{i=1}^{|A_N|}\frac{1}{\sqrt{i}}\ \leqslant\ 2\sqrt{|A_N|}. \end{align*} $$
Therefore,
 $$ \begin{align*} \left\|\sum_{e\in A} e\right\|\ =\ \left(\sum_{N=1}^{\infty}\left\|\sum_{e\in A_N} e\right\|^2\right)^{1/2}\ \leqslant\ 2\left(\sum_{N=1}^{\infty} |A_N|\right)^{1/2}\ =\ 2|A|^{1/2}. \end{align*} $$
$$ \begin{align*} \left\|\sum_{e\in A} e\right\|\ =\ \left(\sum_{N=1}^{\infty}\left\|\sum_{e\in A_N} e\right\|^2\right)^{1/2}\ \leqslant\ 2\left(\sum_{N=1}^{\infty} |A_N|\right)^{1/2}\ =\ 2|A|^{1/2}. \end{align*} $$
We have shown that
![]() $|A|^{1/2}\leqslant \|\sum _{e\in A}e\|\leqslant 2|A|^{1/2}$
, so
$|A|^{1/2}\leqslant \|\sum _{e\in A}e\|\leqslant 2|A|^{1/2}$
, so
![]() $\mathcal {B}$
is democratic.
$\mathcal {B}$
is democratic.
4.2 An
 $(\alpha ,\infty )$
-quasi-greedy basis
$(\alpha ,\infty )$
-quasi-greedy basis
Fix a nonzero
![]() $\alpha \in \omega _1$
and consider the following collection subsets related to
$\alpha \in \omega _1$
and consider the following collection subsets related to
![]() $\mathcal {S}_{\alpha }$
:
$\mathcal {S}_{\alpha }$
:
The family
![]() $\mathcal {F}_1$
(among others) recently appeared in [Reference Beanland, Chu and Finch-Smith10].
$\mathcal {F}_1$
(among others) recently appeared in [Reference Beanland, Chu and Finch-Smith10].
Lemma 4.8 Let
![]() $F \in \mathcal {F}_{\alpha }$
. Then F can be written as the union of two disjoint sets in
$F \in \mathcal {F}_{\alpha }$
. Then F can be written as the union of two disjoint sets in
![]() $\mathcal {S}_{\alpha }$
.
$\mathcal {S}_{\alpha }$
.
Proof Write
![]() $F = \cup _{i=1}^r E_i$
, where
$F = \cup _{i=1}^r E_i$
, where
![]() $r/2 \leqslant E_1 < E_2 < \cdots < E_{r}$
and sets
$r/2 \leqslant E_1 < E_2 < \cdots < E_{r}$
and sets
![]() $E_i\in \mathcal {S}_{\alpha -1}$
. Discard all the empty
$E_i\in \mathcal {S}_{\alpha -1}$
. Discard all the empty
![]() $E_i$
and renumber to have nonempty sets
$E_i$
and renumber to have nonempty sets
![]() $E^{\prime }_i$
satisfying
$E^{\prime }_i$
satisfying
![]() $r/2 \leqslant E_1' < E^{\prime }_2 < \cdots < E^{\prime }_{\ell }$
for some
$r/2 \leqslant E_1' < E^{\prime }_2 < \cdots < E^{\prime }_{\ell }$
for some
![]() $\ell \leqslant r$
. Let
$\ell \leqslant r$
. Let
![]() $s = \lceil r/2\rceil $
.
$s = \lceil r/2\rceil $
.
Case 1:
![]() $s\geqslant \ell $
. Then
$s\geqslant \ell $
. Then
![]() $s\leqslant E_1' < E_2' < \cdots < E^{\prime }_{\ell }$
implies that
$s\leqslant E_1' < E_2' < \cdots < E^{\prime }_{\ell }$
implies that
![]() $F = \cup _{i = 1}^{\ell } E_i'\in \mathcal {S}_{\alpha }$
. We are done.
$F = \cup _{i = 1}^{\ell } E_i'\in \mathcal {S}_{\alpha }$
. We are done.
Case 2:
![]() $s < \ell $
. Let
$s < \ell $
. Let
![]() $F_1 = \cup _{i=1}^s E^{\prime }_i$
, which is in
$F_1 = \cup _{i=1}^s E^{\prime }_i$
, which is in
![]() $S_{\alpha }$
due to Case 1. Note that
$S_{\alpha }$
due to Case 1. Note that
furthermore,
![]() $\ell -s \leqslant r-s \leqslant s+1$
. Therefore,
$\ell -s \leqslant r-s \leqslant s+1$
. Therefore,
![]() $F_2 := \cup _{i=s+1}^{\ell } E^{\prime }_i\in \mathcal {S}_{\alpha }$
. Since
$F_2 := \cup _{i=s+1}^{\ell } E^{\prime }_i\in \mathcal {S}_{\alpha }$
. Since
![]() $F = F_1\cup F_2$
, we are done.
$F = F_1\cup F_2$
, we are done.
Clearly,
![]() $\mathcal {S}_{\alpha }\subset \mathcal {F}_{\alpha }$
. Let
$\mathcal {S}_{\alpha }\subset \mathcal {F}_{\alpha }$
. Let
![]() $X_{\alpha ,\infty }$
be the completion of
$X_{\alpha ,\infty }$
be the completion of
![]() $c_{00}$
under the following norm: for
$c_{00}$
under the following norm: for
![]() $(a_i)\in c_{00}$
,
$(a_i)\in c_{00}$
,
 $$ \begin{align*} \|(a_i)\|_{X_{\alpha,\infty}} :=\ \sup\left\{\sum_{j=1}^d \left|\sum_{i\in I_j}a_i\right|: I_1 < I_2 < \cdots < I_d \mbox{ intervals}, (\min I_j)_{j=1}^d\in \mathcal{F}_{\alpha}\right\}. \end{align*} $$
$$ \begin{align*} \|(a_i)\|_{X_{\alpha,\infty}} :=\ \sup\left\{\sum_{j=1}^d \left|\sum_{i\in I_j}a_i\right|: I_1 < I_2 < \cdots < I_d \mbox{ intervals}, (\min I_j)_{j=1}^d\in \mathcal{F}_{\alpha}\right\}. \end{align*} $$
The space
![]() $X_{\alpha ,\infty }$
above is the Jamesfication of the combinatorial space
$X_{\alpha ,\infty }$
above is the Jamesfication of the combinatorial space
![]() $X[\mathcal {F}_{\alpha }]$
(see [Reference Argyros, Motakis and Sari8, Reference Bellenot, Haydon and Odell11]) and is denoted by
$X[\mathcal {F}_{\alpha }]$
(see [Reference Argyros, Motakis and Sari8, Reference Bellenot, Haydon and Odell11]) and is denoted by
![]() $J(X[\mathcal {F}_{\alpha }])$
.
$J(X[\mathcal {F}_{\alpha }])$
.
Theorem 4.9 The standard basis
![]() $(e_n)$
for the space
$(e_n)$
for the space
![]() $X_{\alpha ,\infty }$
is
$X_{\alpha ,\infty }$
is
![]() $(\alpha ,\infty )$
-quasi-greedy.
$(\alpha ,\infty )$
-quasi-greedy.
We prove the above theorem through the following propositions. Let us start with the easiest one.
Proposition 4.10 The basis
![]() $(e_n)$
is democratic and
$(e_n)$
is democratic and
![]() $\mathcal {F}_{\alpha }$
-unconditional, and thus
$\mathcal {F}_{\alpha }$
-unconditional, and thus
![]() $\mathcal {S}_{\alpha }$
-unconditional.
$\mathcal {S}_{\alpha }$
-unconditional.
Proof It follows directly from the definition of
![]() $\|\cdot \|$
that for
$\|\cdot \|$
that for
![]() $x\in X$
and
$x\in X$
and
![]() $F \in \mathcal {F}_{\alpha }$
,
$F \in \mathcal {F}_{\alpha }$
,
 $$ \begin{align*} \left\|\sum_{i\in F} e_i^*(x)e_i\right\|_{X_{\alpha, \infty}}\ =\ \sum_{i \in F}|e_i^*(x)|\ \leqslant\ \|x\|_{X_{\alpha, \infty}}. \end{align*} $$
$$ \begin{align*} \left\|\sum_{i\in F} e_i^*(x)e_i\right\|_{X_{\alpha, \infty}}\ =\ \sum_{i \in F}|e_i^*(x)|\ \leqslant\ \|x\|_{X_{\alpha, \infty}}. \end{align*} $$
Hence,
![]() $(e_n)$
is
$(e_n)$
is
![]() $\mathcal {F}_{\alpha }$
-unconditional.
$\mathcal {F}_{\alpha }$
-unconditional.
Let
![]() $A, B\subset \mathbb {N}$
with
$A, B\subset \mathbb {N}$
with
![]() $|A| \leqslant |B|$
. By Proposition 1.8, there exists
$|A| \leqslant |B|$
. By Proposition 1.8, there exists
![]() $N\in \mathbb {N}_{\geqslant 6}$
such that
$N\in \mathbb {N}_{\geqslant 6}$
such that
Without loss of generality, assume that
![]() $|B|\geqslant N^2$
. Let
$|B|\geqslant N^2$
. Let
![]() $B'\subset B$
such that
$B'\subset B$
such that
![]() $|B'|\geqslant |B|/2$
and
$|B'|\geqslant |B|/2$
and
![]() $B'\in \mathcal {S}_1\subset \mathcal {F}_1$
. Form
$B'\in \mathcal {S}_1\subset \mathcal {F}_1$
. Form
![]() $B" = B'\backslash \{1, \ldots , N-1\}\in \mathcal {F}_{\alpha }$
. We have
$B" = B'\backslash \{1, \ldots , N-1\}\in \mathcal {F}_{\alpha }$
. We have
Therefore,
![]() $(e_n)$
is democratic.
$(e_n)$
is democratic.
Proposition 4.11 The basis
![]() $(e_n)$
for the space
$(e_n)$
for the space
![]() $X_{\alpha ,\infty }$
is 1-suppression quasi-greedy.
$X_{\alpha ,\infty }$
is 1-suppression quasi-greedy.
Proof Let
![]() $x=(a_i)\in X_{\alpha ,\infty }$
and
$x=(a_i)\in X_{\alpha ,\infty }$
and
![]() $|a_N| = \|x\|_{\infty }$
. By induction, we need only to show that
$|a_N| = \|x\|_{\infty }$
. By induction, we need only to show that
Suppose, for a contradiction, that
![]() $\|x-a_Ne_N\|> \|x\|$
. Removing the Nth coefficient
$\|x-a_Ne_N\|> \|x\|$
. Removing the Nth coefficient
![]() $a_N$
increases the norm implies that there exists an admissible set of intervals
$a_N$
increases the norm implies that there exists an admissible set of intervals
![]() $\{I_j\}_{j=1}^d$
satisfying:
$\{I_j\}_{j=1}^d$
satisfying:
-
(1)
 $a_{\min I_j}a_{\max I_j}\neq 0$
for all
$a_{\min I_j}a_{\max I_j}\neq 0$
for all
 $1\leqslant j\leqslant d$
,
$1\leqslant j\leqslant d$
, -
(2) for some k,
 $N\in I_k$
and
$N\in I_k$
and
 $\min I_k < N < \max I_k$
,
$\min I_k < N < \max I_k$
, -
(3)
 $\sum _{1\leqslant j\leqslant d, j\neq k} |\sum _{i\in I_j}a_i| + |\sum _{i\in I_k, i\neq N}a_i|> \|x\|$
.
$\sum _{1\leqslant j\leqslant d, j\neq k} |\sum _{i\in I_j}a_i| + |\sum _{i\in I_k, i\neq N}a_i|> \|x\|$
.
For two integers
![]() $a \leqslant b$
, let
$a \leqslant b$
, let
![]() $[a, b] = \{a, a+1, \ldots , b\}$
; when
$[a, b] = \{a, a+1, \ldots , b\}$
; when
![]() $a> b$
, we let
$a> b$
, we let
![]() $[a, b] = \emptyset $
. We form a new sequence of intervals as follows: if
$[a, b] = \emptyset $
. We form a new sequence of intervals as follows: if
![]() $k> 1$
,
$k> 1$
,
 $$ \begin{align*}&I_1' \ =\ I_1\backslash \min I_1, I^{\prime}_2 \ =\ I_2, \ldots, I^{\prime}_{k-1} \ =\ I_{k-1},\\ &I^{\prime}_k \ =\ [\min I_k, N-1], I^{\prime}_{k+1} \ =\ \{N\}, I^{\prime}_{k+2} \ =\ [N+1, \max I_k],\\ &I^{\prime}_{k+3}\ =\ I_{k+1}, \ldots, I^{\prime}_{d+2}\ =\ I_{d}. \end{align*} $$
$$ \begin{align*}&I_1' \ =\ I_1\backslash \min I_1, I^{\prime}_2 \ =\ I_2, \ldots, I^{\prime}_{k-1} \ =\ I_{k-1},\\ &I^{\prime}_k \ =\ [\min I_k, N-1], I^{\prime}_{k+1} \ =\ \{N\}, I^{\prime}_{k+2} \ =\ [N+1, \max I_k],\\ &I^{\prime}_{k+3}\ =\ I_{k+1}, \ldots, I^{\prime}_{d+2}\ =\ I_{d}. \end{align*} $$
If
![]() $k= 1$
, then
$k= 1$
, then
 $$ \begin{align*} &I^{\prime}_1 \ =\ [\min I_1 + 1, N-1], I^{\prime}_2 \ =\ \{N\}, I^{\prime}_{3}\ =\ [N+1, \max I_1],\\ &I^{\prime}_{4}\ =\ I_{2}, \ldots, I^{\prime}_{d+2}\ =\ I_d. \end{align*} $$
$$ \begin{align*} &I^{\prime}_1 \ =\ [\min I_1 + 1, N-1], I^{\prime}_2 \ =\ \{N\}, I^{\prime}_{3}\ =\ [N+1, \max I_1],\\ &I^{\prime}_{4}\ =\ I_{2}, \ldots, I^{\prime}_{d+2}\ =\ I_d. \end{align*} $$
To see that
![]() $\{I_j'\}_{j=1}^{d+2}$
is admissible, we need to show
$\{I_j'\}_{j=1}^{d+2}$
is admissible, we need to show
![]() $\{\min I_j'\}_{j=1}^{d+2}\in \mathcal {F}_{\alpha }$
. We consider only the case when
$\{\min I_j'\}_{j=1}^{d+2}\in \mathcal {F}_{\alpha }$
. We consider only the case when
![]() $k> 1$
; the case
$k> 1$
; the case
![]() $k = 1$
is similar. By construction,
$k = 1$
is similar. By construction,
Let
![]() $A = \{\min I_j\}_{j=1}^d$
and
$A = \{\min I_j\}_{j=1}^d$
and
![]() $B = \{\min (I_1\backslash \min I_1)\}\cup \{\min I_j\,:\, 2\leqslant j\leqslant d\}$
. Since
$B = \{\min (I_1\backslash \min I_1)\}\cup \{\min I_j\,:\, 2\leqslant j\leqslant d\}$
. Since
![]() $\min B-\min A\geqslant 1$
and
$\min B-\min A\geqslant 1$
and
![]() $A\in \mathcal {F}_{\alpha }$
, we know that
$A\in \mathcal {F}_{\alpha }$
, we know that
![]() $B\cup \{N, N+1\}\in \mathcal {F}_{\alpha }$
.
$B\cup \{N, N+1\}\in \mathcal {F}_{\alpha }$
.
We now use the admissible set
![]() $(I^{\prime }_j)_{j=1}^{d+2}$
to obtain a contradiction. Write
$(I^{\prime }_j)_{j=1}^{d+2}$
to obtain a contradiction. Write
 $$ \begin{align}\|x\|\ \geqslant\ \sum_{j=1}^{d+2}\left|\sum_{i\in I^{\prime}_j}a_i\right| \ =\ \sum_{j = 1, k , k+1, k+2}\left|\sum_{i\in I^{\prime}_j}a_i\right| + \sum_{j\neq 1, k, k+1, k+2}\left|\sum_{i\in I^{\prime}_j}a_i\right|.\end{align} $$
$$ \begin{align}\|x\|\ \geqslant\ \sum_{j=1}^{d+2}\left|\sum_{i\in I^{\prime}_j}a_i\right| \ =\ \sum_{j = 1, k , k+1, k+2}\left|\sum_{i\in I^{\prime}_j}a_i\right| + \sum_{j\neq 1, k, k+1, k+2}\left|\sum_{i\in I^{\prime}_j}a_i\right|.\end{align} $$
Since
![]() $|a_N|\geqslant |a_{\min I_1}|$
, we have
$|a_N|\geqslant |a_{\min I_1}|$
, we have
 $$ \begin{align}\sum_{j = 1, k , k+1, k+2}\left|\sum_{i\in I^{\prime}_j}a_i\right|&\ \geqslant\ \left(\left|\sum_{i\in I_1}a_i\right|-|a_{\min I_1}|\right) + \left|\sum_{i=\min I_k}^{N-1}a_i\right| + |a_N| + \left|\sum_{i=N+1}^{\max I_k}a_i\right|\nonumber\\ &\ \geqslant\ \left|\sum_{i\in I_1}a_i\right| + \left|\sum_{i\in I_k, i\neq N}a_i\right|. \end{align} $$
$$ \begin{align}\sum_{j = 1, k , k+1, k+2}\left|\sum_{i\in I^{\prime}_j}a_i\right|&\ \geqslant\ \left(\left|\sum_{i\in I_1}a_i\right|-|a_{\min I_1}|\right) + \left|\sum_{i=\min I_k}^{N-1}a_i\right| + |a_N| + \left|\sum_{i=N+1}^{\max I_k}a_i\right|\nonumber\\ &\ \geqslant\ \left|\sum_{i\in I_1}a_i\right| + \left|\sum_{i\in I_k, i\neq N}a_i\right|. \end{align} $$
Furthermore, by definition,
 $$ \begin{align}\sum_{j\neq 1, k, k+1, k+2}\left|\sum_{i\in I^{\prime}_j}a_i\right|\ =\ \sum_{j = 2}^{k-1}\left|\sum_{i\in I_j}a_i\right| + \sum_{j=k+1}^{d}\left|\sum_{i\in I_j}a_i\right|.\end{align} $$
$$ \begin{align}\sum_{j\neq 1, k, k+1, k+2}\left|\sum_{i\in I^{\prime}_j}a_i\right|\ =\ \sum_{j = 2}^{k-1}\left|\sum_{i\in I_j}a_i\right| + \sum_{j=k+1}^{d}\left|\sum_{i\in I_j}a_i\right|.\end{align} $$
By (4.1)–(4.3), we conclude that
 $$ \begin{align*}\|x\|\ \geqslant\ \sum_{1\leqslant j\leqslant d, j\neq k} \left|\sum_{i\in I_j}a_i\right| + \left|\sum_{i\in I_k, i\neq N}a_i\right|\> \ \|x\|,\end{align*} $$
$$ \begin{align*}\|x\|\ \geqslant\ \sum_{1\leqslant j\leqslant d, j\neq k} \left|\sum_{i\in I_j}a_i\right| + \left|\sum_{i\in I_k, i\neq N}a_i\right|\> \ \|x\|,\end{align*} $$
which is a contradiction. Therefore,
![]() $(e_n)$
is a
$(e_n)$
is a
![]() $1$
-suppression quasi-greedy.
$1$
-suppression quasi-greedy.
Corollary 4.12 The basis
![]() $(e_n)$
is
$(e_n)$
is
![]() $\mathcal {F}_{\alpha }$
-greedy and, thus, is
$\mathcal {F}_{\alpha }$
-greedy and, thus, is
![]() $\mathcal {S}_{\alpha }$
-greedy.
$\mathcal {S}_{\alpha }$
-greedy.
It remains to show that
![]() $(e_n)$
is not
$(e_n)$
is not
![]() $\mathcal {S}_{\alpha +1}$
-unconditional and, thus, not
$\mathcal {S}_{\alpha +1}$
-unconditional and, thus, not
![]() $\mathcal {S}_{\alpha +1}$
-greedy. This part of the proof will require the repeated averages hierarchy [Reference Argyros, Godefroy, Rosenthal, Johnson and Lindenstrauss6, p. 1053]. However, for our purposes, we only need the following lemma, a weaker result than [Reference Argyros and Tolias9, Proposition 12.9].
$\mathcal {S}_{\alpha +1}$
-greedy. This part of the proof will require the repeated averages hierarchy [Reference Argyros, Godefroy, Rosenthal, Johnson and Lindenstrauss6, p. 1053]. However, for our purposes, we only need the following lemma, a weaker result than [Reference Argyros and Tolias9, Proposition 12.9].
Lemma 4.13 For each
![]() $\alpha \in \omega _1$
,
$\alpha \in \omega _1$
,
![]() $\varepsilon>0$
, and
$\varepsilon>0$
, and
![]() $N\in \mathbb {N}$
, there is a sequence
$N\in \mathbb {N}$
, there is a sequence
![]() $(a^{\alpha }_k)_{k=1}^{\infty }$
satisfying:
$(a^{\alpha }_k)_{k=1}^{\infty }$
satisfying:
-
(1)
 $a_k^{\alpha } \geqslant 0$
for each
$a_k^{\alpha } \geqslant 0$
for each
 $k\in \mathbb {N}$
and
$k\in \mathbb {N}$
and
 $\|(a^{\alpha }_k)_k\|_{\ell _1}=1$
,
$\|(a^{\alpha }_k)_k\|_{\ell _1}=1$
, -
(2)
 $\{k : a^{\alpha }_k\neq 0\}$
is an interval and a maximal
$\{k : a^{\alpha }_k\neq 0\}$
is an interval and a maximal
 $\mathcal {S}_{\alpha +1}$
-set,
$\mathcal {S}_{\alpha +1}$
-set, -
(3)
 $L:= \min \{k: a^{\alpha }_k\neq 0\}> N$
and
$L:= \min \{k: a^{\alpha }_k\neq 0\}> N$
and
 $(a^{\alpha }_k)_{k\geqslant L}$
is monotone decreasing,
$(a^{\alpha }_k)_{k\geqslant L}$
is monotone decreasing, -
(4) for each
 $G \in \mathcal {S}_{\alpha }$
, we have
$G \in \mathcal {S}_{\alpha }$
, we have
 $\sum _{k \in G} a_k^{\alpha } <\varepsilon $
.
$\sum _{k \in G} a_k^{\alpha } <\varepsilon $
.
Choose N such that
Fix
![]() $\varepsilon>0$
and find
$\varepsilon>0$
and find
![]() $(a_k^{\alpha })$
satisfying Lemma 4.13 with N chosen as above. Since
$(a_k^{\alpha })$
satisfying Lemma 4.13 with N chosen as above. Since
![]() ${F=\{k : a_k^{\alpha }\not =0\}\in \mathcal {S}_{\alpha +1}}$
, write
${F=\{k : a_k^{\alpha }\not =0\}\in \mathcal {S}_{\alpha +1}}$
, write
![]() $F = \cup _{i=1}^m E_i$
, where
$F = \cup _{i=1}^m E_i$
, where
![]() $m\leqslant E_1 < E_2 <\cdots < E_m$
and
$m\leqslant E_1 < E_2 <\cdots < E_m$
and
![]() $E_i\in \mathcal {S}_{\alpha }$
. Since F is an interval, each
$E_i\in \mathcal {S}_{\alpha }$
. Since F is an interval, each
![]() $E_i$
is an interval; furthermore,
$E_i$
is an interval; furthermore,
![]() $N < \{\min E_i: 1\leqslant i\leqslant m\}\in \mathcal {S}_1$
. Hence,
$N < \{\min E_i: 1\leqslant i\leqslant m\}\in \mathcal {S}_1$
. Hence,
![]() $\{\min E_i: 1\leqslant i\leqslant m\}\in \mathcal {S}_{\alpha }\subset \mathcal {F}_{\alpha }$
. By Lemma 4.13(1) and (2), we have
$\{\min E_i: 1\leqslant i\leqslant m\}\in \mathcal {S}_{\alpha }\subset \mathcal {F}_{\alpha }$
. By Lemma 4.13(1) and (2), we have
![]() $\|\sum _{k\in F}a_k^{\alpha } e_k\| = 1$
.
$\|\sum _{k\in F}a_k^{\alpha } e_k\| = 1$
.
We estimate
![]() $\sum _{k\in F}(-1)^k a_k^{\alpha } e_k$
. Let
$\sum _{k\in F}(-1)^k a_k^{\alpha } e_k$
. Let
![]() $I_1<\cdots < I_d$
be intervals so that
$I_1<\cdots < I_d$
be intervals so that
![]() $(\min I_j)_{j=1}^d \in \mathcal {F}_{\alpha }$
and
$(\min I_j)_{j=1}^d \in \mathcal {F}_{\alpha }$
and
![]() $a^{\alpha }_{\min I_j}\neq 0$
. For any interval
$a^{\alpha }_{\min I_j}\neq 0$
. For any interval
![]() $I_j$
,
$I_j$
,
![]() $|\sum _{i\in I_j}(-1)^k a_k^{\alpha }|\leqslant 2a^{\alpha }_{\min I_j}$
because
$|\sum _{i\in I_j}(-1)^k a_k^{\alpha }|\leqslant 2a^{\alpha }_{\min I_j}$
because
![]() $(a^{\alpha }_k)_k$
is monotone decreasing. Therefore,
$(a^{\alpha }_k)_k$
is monotone decreasing. Therefore,
 $$ \begin{align*}\sum_{j=1}^d \left|\sum_{k\in I_j}(-1)^k a_k^{\alpha}\right|\ \leqslant\ \sum_{j=1}^d 2 a^{\alpha}_{\min I_j}.\end{align*} $$
$$ \begin{align*}\sum_{j=1}^d \left|\sum_{k\in I_j}(-1)^k a_k^{\alpha}\right|\ \leqslant\ \sum_{j=1}^d 2 a^{\alpha}_{\min I_j}.\end{align*} $$
By Lemma 4.8, we can write the set
![]() $\{\min I_1, \min I_{2}, \ldots , \min {I_d}\}$
as the union of two disjoint sets
$\{\min I_1, \min I_{2}, \ldots , \min {I_d}\}$
as the union of two disjoint sets
![]() $A_1$
and
$A_1$
and
![]() $A_2$
in
$A_2$
in
![]() $\mathcal {S}_{\alpha }$
. By Lemma 4.13(3), we obtain
$\mathcal {S}_{\alpha }$
. By Lemma 4.13(3), we obtain
 $$ \begin{align*}\sum_{j=1}^d a^{\alpha}_{\min I_j}\ =\ \sum_{i\in A_1}a^{\alpha}_i + \sum_{i\in A_2}a^{\alpha}_i\ <\ 2\varepsilon.\end{align*} $$
$$ \begin{align*}\sum_{j=1}^d a^{\alpha}_{\min I_j}\ =\ \sum_{i\in A_1}a^{\alpha}_i + \sum_{i\in A_2}a^{\alpha}_i\ <\ 2\varepsilon.\end{align*} $$
Thus,
![]() $\|\sum _{k\in F}(-1)^k a_k^{\alpha } e_k\| < 4\varepsilon $
. As
$\|\sum _{k\in F}(-1)^k a_k^{\alpha } e_k\| < 4\varepsilon $
. As
![]() $\varepsilon $
was arbitrary and
$\varepsilon $
was arbitrary and
![]() $F\in \mathcal {S}_{\alpha +1}$
, we see that
$F\in \mathcal {S}_{\alpha +1}$
, we see that
![]() $(e_n)$
is not
$(e_n)$
is not
![]() $\mathcal {S}_{\alpha +1}$
-unconditional.
$\mathcal {S}_{\alpha +1}$
-unconditional.
4.3 An
 $(\infty ,\alpha )$
-quasi-greedy basis
$(\infty ,\alpha )$
-quasi-greedy basis
4.3.1 Repeated average hierarchy
Let
![]() $[\mathbb {N}]$
denote the collection of all infinite subsequences of
$[\mathbb {N}]$
denote the collection of all infinite subsequences of
![]() $\mathbb {N}$
. Similarly, if
$\mathbb {N}$
. Similarly, if
![]() $M\in [\mathbb {N}]$
, then
$M\in [\mathbb {N}]$
, then
![]() $[M]$
denotes the collection of all infinite subsequences of M.
$[M]$
denotes the collection of all infinite subsequences of M.
Definition 4.14 Let
![]() $\mathcal {B} = (e_n)$
be the canonical basis of
$\mathcal {B} = (e_n)$
be the canonical basis of
![]() $c_{00}$
. For every countable ordinal
$c_{00}$
. For every countable ordinal
![]() $\alpha $
and
$\alpha $
and
![]() $M = (m_n)_{n=1}^{\infty }\in [\mathbb {N}]$
, we define a convex block sequence
$M = (m_n)_{n=1}^{\infty }\in [\mathbb {N}]$
, we define a convex block sequence
![]() $(\alpha (M, n))_{n=1}^{\infty }$
of
$(\alpha (M, n))_{n=1}^{\infty }$
of
![]() $\mathcal {B}$
by transfinite induction on
$\mathcal {B}$
by transfinite induction on
![]() $\alpha $
. If
$\alpha $
. If
![]() $\alpha = 0$
, then
$\alpha = 0$
, then
![]() $\alpha (M, n) := e_{m_n}$
. Assume that
$\alpha (M, n) := e_{m_n}$
. Assume that
![]() $(\beta (M, n))_{n=1}^{\infty }$
has been defined for all
$(\beta (M, n))_{n=1}^{\infty }$
has been defined for all
![]() $\beta < \alpha $
and all
$\beta < \alpha $
and all
![]() $M\in [\mathbb {N}]$
. For
$M\in [\mathbb {N}]$
. For
![]() $M\in [\mathbb {N}]$
, we define
$M\in [\mathbb {N}]$
, we define
![]() $(\alpha (M, n))_{n=1}^{\infty }$
.
$(\alpha (M, n))_{n=1}^{\infty }$
.
If
![]() $\alpha $
is a successor ordinal, write
$\alpha $
is a successor ordinal, write
![]() $\alpha = \beta + 1$
. Set
$\alpha = \beta + 1$
. Set
 $$ \begin{align*}\alpha(M, 1)\ :=\ \frac{1}{m_1}\sum_{n=1}^{m_1}\beta(M, n).\end{align*} $$
$$ \begin{align*}\alpha(M, 1)\ :=\ \frac{1}{m_1}\sum_{n=1}^{m_1}\beta(M, n).\end{align*} $$
Suppose that
![]() $\alpha (M,1) < \cdots < \alpha (M,n)$
have been defined. Let
$\alpha (M,1) < \cdots < \alpha (M,n)$
have been defined. Let
Set
 $$ \begin{align*}\alpha(M, n+1)\ :=\ \frac{1}{k_n}\sum_{i=1}^{k_n} \beta(M_{n+1}, i).\end{align*} $$
$$ \begin{align*}\alpha(M, n+1)\ :=\ \frac{1}{k_n}\sum_{i=1}^{k_n} \beta(M_{n+1}, i).\end{align*} $$
If
![]() $\alpha $
is a limit ordinal, let
$\alpha $
is a limit ordinal, let
![]() $(\alpha _n+1)\nearrow \alpha $
. Set
$(\alpha _n+1)\nearrow \alpha $
. Set
Suppose that
![]() $\alpha (M,1) < \cdots < \alpha (M,n)$
have been defined. Let
$\alpha (M,1) < \cdots < \alpha (M,n)$
have been defined. Let
Set
Lemma 4.15 For each ordinal
![]() $\alpha \geqslant 1$
and
$\alpha \geqslant 1$
and
![]() $M\in [\mathbb {N}]$
, we have
$M\in [\mathbb {N}]$
, we have
Proof The proof is immediate from induction.
Proposition 4.16 Fix
![]() $\alpha < \beta $
. For all
$\alpha < \beta $
. For all
![]() $N\in \mathbb {N}$
and
$N\in \mathbb {N}$
and
![]() $M\in [\mathbb {N}]$
, there exists
$M\in [\mathbb {N}]$
, there exists
![]() $L\in [M]$
such that
$L\in [M]$
such that
![]() $\min L> N$
and
$\min L> N$
and
where
Remark 4.17 See [Reference Argyros and Tolias9, Proposition 2.3] for the case when
![]() $\alpha $
is a finite ordinal. Our proof of Proposition 4.16 is a combination of ideas used in the proofs of [Reference Argyros and Tolias9, Proposition 2.3] and [Reference Argyros and Gasparis5, Proposition 2.15].
$\alpha $
is a finite ordinal. Our proof of Proposition 4.16 is a combination of ideas used in the proofs of [Reference Argyros and Tolias9, Proposition 2.3] and [Reference Argyros and Gasparis5, Proposition 2.15].
Proof of Proposition 4.16
We prove by transfinite induction on
![]() $\beta $
. Base case:
$\beta $
. Base case:
![]() ${\beta = 1}$
. Then
${\beta = 1}$
. Then
![]() $\alpha = 0$
. Let
$\alpha = 0$
. Let
![]() $N\in \mathbb {N}$
and
$N\in \mathbb {N}$
and
![]() $M = (m_n)_{n=1}^{\infty }\in [\mathbb {N}]$
. Let
$M = (m_n)_{n=1}^{\infty }\in [\mathbb {N}]$
. Let
![]() $m_k$
be the smallest such that
$m_k$
be the smallest such that
![]() ${m_k> N}$
. Choose
${m_k> N}$
. Choose
![]() $L = (m_n)_{n\geqslant k}$
. We have
$L = (m_n)_{n\geqslant k}$
. We have
Indeed, for finite ordinals
![]() $\beta \geqslant 1$
, we know the conclusion holds by [Reference Argyros and Tolias9, Proposition 2.3]. Inductive hypothesis: suppose that the statement holds for all
$\beta \geqslant 1$
, we know the conclusion holds by [Reference Argyros and Tolias9, Proposition 2.3]. Inductive hypothesis: suppose that the statement holds for all
![]() $\eta < \beta $
for some
$\eta < \beta $
for some
![]() $\beta \geqslant \omega $
. We need to show that it also holds for
$\beta \geqslant \omega $
. We need to show that it also holds for
![]() $\beta $
.
$\beta $
.
Case 1:
![]() $\beta $
is a limit ordinal. Let
$\beta $
is a limit ordinal. Let
![]() $(\beta _n + 1)\nearrow \beta $
and
$(\beta _n + 1)\nearrow \beta $
and
![]() $\alpha < \beta $
. Choose
$\alpha < \beta $
. Choose
![]() $m> N$
such that
$m> N$
such that
![]() $\beta _m> \alpha $
. Set
$\beta _m> \alpha $
. Set
![]() $L_1 := M|_{> m}$
and
$L_1 := M|_{> m}$
and
![]() $\ell := \min L_1> m$
. Note that
$\ell := \min L_1> m$
. Note that
![]() $\ell \geqslant 3$
. By the inductive hypothesis, there exists
$\ell \geqslant 3$
. By the inductive hypothesis, there exists
![]() $L_2\in [M]$
such that
$L_2\in [M]$
such that
![]() $\min L_2> \max \operatorname {\mathrm {supp}}(\beta _{\ell }(L_1, 1))$
and
$\min L_2> \max \operatorname {\mathrm {supp}}(\beta _{\ell }(L_1, 1))$
and
Repeat the process to find subsequences
![]() $L_3, \ldots , L_{\ell }\in [M]$
such that
$L_3, \ldots , L_{\ell }\in [M]$
such that
and
Let
![]() $L:= \cup _{n=1}^{\ell -1}\operatorname {\mathrm {supp}} (\beta _{\ell }(L_n, 1))\cup L_{\ell }\in [M]$
. Then
$L:= \cup _{n=1}^{\ell -1}\operatorname {\mathrm {supp}} (\beta _{\ell }(L_n, 1))\cup L_{\ell }\in [M]$
. Then
![]() $\min L> N$
. By definition,
$\min L> N$
. By definition,
 $$ \begin{align*}\beta(L, 1)\ :=\ (\beta_{\ell}+1)(L, 1)\ =\ \frac{1}{\ell}\sum_{n=1}^{\ell} \beta_{\ell}(L, n)\ =\ \frac{1}{\ell} \sum_{n=1}^{\ell} \beta_{\ell}(L_n, 1).\end{align*} $$
$$ \begin{align*}\beta(L, 1)\ :=\ (\beta_{\ell}+1)(L, 1)\ =\ \frac{1}{\ell}\sum_{n=1}^{\ell} \beta_{\ell}(L, n)\ =\ \frac{1}{\ell} \sum_{n=1}^{\ell} \beta_{\ell}(L_n, 1).\end{align*} $$
We have
 $$ \begin{align*} \|\beta(L, 1)\|_{\alpha}&\ \leqslant\ \frac{1}{\ell} \sum_{n=1}^{\ell} \|\beta_{\ell}(L_n, 1)\|_{\alpha}\\ &\ \leqslant\ \frac{1}{\ell}+ \frac{1}{\ell} \left(\frac{3}{\min L_2} + \cdots + \frac{3}{\min L_{\ell}}\right)\\ &\ \leqslant\ \frac{1}{\ell} + \frac{1}{\ell} \frac{3}{\min L_2}\left(1 + \frac{1}{8} + \frac{1}{8^2} + \cdots\right)\mbox{ by Lemma}\ \mbox{A.2}\\ &\ =\ \frac{1}{\ell}\left(1+\frac{24}{7\min L_2}\right) \ <\ \frac{3}{\ell}. \end{align*} $$
$$ \begin{align*} \|\beta(L, 1)\|_{\alpha}&\ \leqslant\ \frac{1}{\ell} \sum_{n=1}^{\ell} \|\beta_{\ell}(L_n, 1)\|_{\alpha}\\ &\ \leqslant\ \frac{1}{\ell}+ \frac{1}{\ell} \left(\frac{3}{\min L_2} + \cdots + \frac{3}{\min L_{\ell}}\right)\\ &\ \leqslant\ \frac{1}{\ell} + \frac{1}{\ell} \frac{3}{\min L_2}\left(1 + \frac{1}{8} + \frac{1}{8^2} + \cdots\right)\mbox{ by Lemma}\ \mbox{A.2}\\ &\ =\ \frac{1}{\ell}\left(1+\frac{24}{7\min L_2}\right) \ <\ \frac{3}{\ell}. \end{align*} $$
Case 2:
![]() $\beta $
is a successor ordinal. Write
$\beta $
is a successor ordinal. Write
![]() $\beta = \eta + 1$
.
$\beta = \eta + 1$
.
-
(1) Case 2.1:
 $\alpha < \eta $
. Set
$\alpha < \eta $
. Set
 $L_1:= M|_{>{N+1}}$
and
$L_1:= M|_{>{N+1}}$
and
 $\ell := \min L_1 \geqslant 3$
. By the inductive hypothesis, there exists
$\ell := \min L_1 \geqslant 3$
. By the inductive hypothesis, there exists
 $L_2\in [M]$
such that
$L_2\in [M]$
such that
 $\min L_2> \max \operatorname {\mathrm {supp}}(\eta (L_1, 1))$
and
$\min L_2> \max \operatorname {\mathrm {supp}}(\eta (L_1, 1))$
and  $$ \begin{align*}\|\eta(L_2, 1)\|_{\alpha} \ <\ \frac{3}{\min L_2}.\end{align*} $$
$$ \begin{align*}\|\eta(L_2, 1)\|_{\alpha} \ <\ \frac{3}{\min L_2}.\end{align*} $$
Repeat the process to find subsequences
 $L_3, \ldots , L_{\ell }$
such that
$L_3, \ldots , L_{\ell }$
such that  $$ \begin{align*}\operatorname{\mathrm{supp}}(\eta(L_1, 1)) \ <\ \operatorname{\mathrm{supp}}(\eta(L_2, 1)) \ <\ \cdots < \ \operatorname{\mathrm{supp}}(\eta(L_{\ell}, 1))\end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{supp}}(\eta(L_1, 1)) \ <\ \operatorname{\mathrm{supp}}(\eta(L_2, 1)) \ <\ \cdots < \ \operatorname{\mathrm{supp}}(\eta(L_{\ell}, 1))\end{align*} $$
and
 $$ \begin{align*}\|\eta(L_n, 1)\|_{\alpha} \ <\ \frac{3}{\min L_n}, \forall 2\leqslant n\leqslant \ell.\end{align*} $$
$$ \begin{align*}\|\eta(L_n, 1)\|_{\alpha} \ <\ \frac{3}{\min L_n}, \forall 2\leqslant n\leqslant \ell.\end{align*} $$
Let
 $L:= \cup _{n=1}^{\ell -1}\operatorname {\mathrm {supp}} (\eta (L_n, 1))\cup L_{\ell }\in [M]$
. Then
$L:= \cup _{n=1}^{\ell -1}\operatorname {\mathrm {supp}} (\eta (L_n, 1))\cup L_{\ell }\in [M]$
. Then
 $\min L> N$
. By definition,
$\min L> N$
. By definition,  $$ \begin{align*}\beta(L, 1)\ :=\ (\eta+1)(L, 1)\ =\ \frac{1}{\ell}\sum_{n=1}^{\ell} \eta(L, n)\ =\ \frac{1}{\ell} \sum_{n=1}^{\ell} \eta(L_n, 1).\end{align*} $$
$$ \begin{align*}\beta(L, 1)\ :=\ (\eta+1)(L, 1)\ =\ \frac{1}{\ell}\sum_{n=1}^{\ell} \eta(L, n)\ =\ \frac{1}{\ell} \sum_{n=1}^{\ell} \eta(L_n, 1).\end{align*} $$
Similar to Case 1, we have
 $\|\beta (L, 1)\|_{\alpha } < 3/\ell $
.
$\|\beta (L, 1)\|_{\alpha } < 3/\ell $
. -
(2) Case 2.2:
 $\alpha = \eta $
. Let
$\alpha = \eta $
. Let
 $(\alpha _n+1)\nearrow \alpha $
and
$(\alpha _n+1)\nearrow \alpha $
and
 $\mathcal {S}_{\alpha _n}\subset \mathcal {S}_{\alpha _{n+1}}$
for all
$\mathcal {S}_{\alpha _n}\subset \mathcal {S}_{\alpha _{n+1}}$
for all
 $n\geqslant 1$
. Set
$n\geqslant 1$
. Set
 $L_1:= M|_{>{N+1}}$
and
$L_1:= M|_{>{N+1}}$
and
 $\ell := \min L_1 \geqslant 3$
. We have
$\ell := \min L_1 \geqslant 3$
. We have  $$ \begin{align*}(\alpha_{\ell}+1)(L_1, 1)\ =\ \alpha(L_1, 1).\end{align*} $$
$$ \begin{align*}(\alpha_{\ell}+1)(L_1, 1)\ =\ \alpha(L_1, 1).\end{align*} $$
Let
 $k_1 = \max \operatorname {\mathrm {supp}} (\alpha (L_1, 1))$
. By the inductive hypothesis, find
$k_1 = \max \operatorname {\mathrm {supp}} (\alpha (L_1, 1))$
. By the inductive hypothesis, find
 $L_2\in [M]$
with
$L_2\in [M]$
with
 $k_1 < \min L_2$
and
$k_1 < \min L_2$
and  $$ \begin{align*}\|\alpha(L_2, 1)\|_{\alpha_{k_1}} \ <\ \frac{3}{\min L_2}.\end{align*} $$
$$ \begin{align*}\|\alpha(L_2, 1)\|_{\alpha_{k_1}} \ <\ \frac{3}{\min L_2}.\end{align*} $$
Repeat the process to find subsequences
 $L_3, \ldots , L_{\ell }\in [M]$
such that
$L_3, \ldots , L_{\ell }\in [M]$
such that  $$ \begin{align*}\operatorname{\mathrm{supp}}(\alpha(L_1, 1)) \ <\ \operatorname{\mathrm{supp}}(\alpha(L_2, 1)) \ <\ \cdots < \ \operatorname{\mathrm{supp}}(\alpha(L_{\ell}, 1))\end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{supp}}(\alpha(L_1, 1)) \ <\ \operatorname{\mathrm{supp}}(\alpha(L_2, 1)) \ <\ \cdots < \ \operatorname{\mathrm{supp}}(\alpha(L_{\ell}, 1))\end{align*} $$
and if
 $k_n = \max \operatorname {\mathrm {supp}} (\alpha (L_n, 1))$
, we have
$k_n = \max \operatorname {\mathrm {supp}} (\alpha (L_n, 1))$
, we have  $$ \begin{align*}\|\alpha(L_n, 1)\|_{\alpha_{k_{n-1}}} \ <\ \frac{3}{\min L_n}, \forall 2\leqslant n\leqslant \ell.\end{align*} $$
$$ \begin{align*}\|\alpha(L_n, 1)\|_{\alpha_{k_{n-1}}} \ <\ \frac{3}{\min L_n}, \forall 2\leqslant n\leqslant \ell.\end{align*} $$
Let
 $L:= \cup _{n=1}^{\ell -1}\operatorname {\mathrm {supp}} (\alpha (L_n, 1))\cup L_{\ell }\in [M]$
. Then
$L:= \cup _{n=1}^{\ell -1}\operatorname {\mathrm {supp}} (\alpha (L_n, 1))\cup L_{\ell }\in [M]$
. Then
 $\beta (L, 1)\ :=\ \frac {1}{\ell }\sum _{n=1}^{\ell } \alpha (L_n, 1)$
.
$\beta (L, 1)\ :=\ \frac {1}{\ell }\sum _{n=1}^{\ell } \alpha (L_n, 1)$
.It holds that
 $\|\beta (L, 1)\|_{\alpha } < \frac {3}{\ell }$
. Indeed, let
$\|\beta (L, 1)\|_{\alpha } < \frac {3}{\ell }$
. Indeed, let
 $G\in \mathcal {S}_{\alpha }$
. Suppose that
$G\in \mathcal {S}_{\alpha }$
. Suppose that
 $k:=\min G\in \operatorname {\mathrm {supp}}(\alpha (L_{j_0}, 1))$
. Then
$k:=\min G\in \operatorname {\mathrm {supp}}(\alpha (L_{j_0}, 1))$
. Then
 $k\leqslant k_{j_0}$
. By the definition of
$k\leqslant k_{j_0}$
. By the definition of
 $\mathcal {S}_{\alpha }$
, choose
$\mathcal {S}_{\alpha }$
, choose
 $p\leqslant k$
such that
$p\leqslant k$
such that
 $G\in \mathcal {S}_{\alpha _p + 1}$
. Finally, let
$G\in \mathcal {S}_{\alpha _p + 1}$
. Finally, let
 $q\leqslant k$
be such that
$q\leqslant k$
be such that
 $G = \cup _{n=1}^q G_n$
, where
$G = \cup _{n=1}^q G_n$
, where
 $G_1 < G_2 < \cdots < G_q$
and
$G_1 < G_2 < \cdots < G_q$
and
 $G_n\in \mathcal {S}_{\alpha _p}$
. For
$G_n\in \mathcal {S}_{\alpha _p}$
. For
 $j_0< n \leqslant \ell $
, because
$j_0< n \leqslant \ell $
, because
 $p\leqslant k\leqslant k_{n-1}$
, we obtain
$p\leqslant k\leqslant k_{n-1}$
, we obtain
 $\mathcal {S}_{\alpha _p}\subset \mathcal {S}_{\alpha _{k_{n-1}}}$
and
$\mathcal {S}_{\alpha _p}\subset \mathcal {S}_{\alpha _{k_{n-1}}}$
and  $$ \begin{align*}\|\alpha(L_n, 1)\|_{\alpha_p}\ \leqslant\ \|\alpha(L_n, 1)\|_{\alpha_{k_{n-1}}} \ <\ \frac{3}{\min L_n}.\end{align*} $$
$$ \begin{align*}\|\alpha(L_n, 1)\|_{\alpha_p}\ \leqslant\ \|\alpha(L_n, 1)\|_{\alpha_{k_{n-1}}} \ <\ \frac{3}{\min L_n}.\end{align*} $$
Therefore,
 $$ \begin{align*}\sum_{n\in G}e_n^*(\alpha(L_n, 1))\ \leqslant\ q\frac{3}{\min L_n}, \forall j_0< n \leqslant \ell.\end{align*} $$
$$ \begin{align*}\sum_{n\in G}e_n^*(\alpha(L_n, 1))\ \leqslant\ q\frac{3}{\min L_n}, \forall j_0< n \leqslant \ell.\end{align*} $$
Noting that
 $q \leqslant k\leqslant k_{j_0}< \min L_{j_0+1}\leqslant \frac {1}{8} \min L_{j_0+2}$
by Lemma A.2, we have
$q \leqslant k\leqslant k_{j_0}< \min L_{j_0+1}\leqslant \frac {1}{8} \min L_{j_0+2}$
by Lemma A.2, we have  $$ \begin{align*}\sum_{n\in G}e_n^*(\beta(L, 1))&\ =\ \frac{1}{\ell}\left(1+1+ 3q\sum_{n=j_0+2}^{\ell} \frac{1}{\min L_n}\right)\\ &\ \leqslant\ \frac{1}{\ell}\left(2 + \frac{24q}{7\min L_{j_0+2}}\right)\ <\ \frac{3}{\ell}. \end{align*} $$
$$ \begin{align*}\sum_{n\in G}e_n^*(\beta(L, 1))&\ =\ \frac{1}{\ell}\left(1+1+ 3q\sum_{n=j_0+2}^{\ell} \frac{1}{\min L_n}\right)\\ &\ \leqslant\ \frac{1}{\ell}\left(2 + \frac{24q}{7\min L_{j_0+2}}\right)\ <\ \frac{3}{\ell}. \end{align*} $$
We have completed the proof.
4.3.2 An
 $(\infty , \alpha )$
-quasi-greedy basis
$(\infty , \alpha )$
-quasi-greedy basis
By Proposition 4.16, we can find infinitely many
![]() $\mathcal {S}_{\alpha +1}$
-maximal sets
$\mathcal {S}_{\alpha +1}$
-maximal sets
![]() $F_1 < F_2 < F_3 < \cdots $
and for each set
$F_1 < F_2 < F_3 < \cdots $
and for each set
![]() $F_i$
, coefficients
$F_i$
, coefficients
![]() $(w_n)_{n\in F_i}$
, such that
$(w_n)_{n\in F_i}$
, such that
![]() $\sum _{n\in F_i} w_n = 1$
, while
$\sum _{n\in F_i} w_n = 1$
, while
 $$ \begin{align*} \left\|\min F_i\cdot \sum_{n\in F_i}w_ne_n\right\|_{\alpha}\ <\ 3. \end{align*} $$
$$ \begin{align*} \left\|\min F_i\cdot \sum_{n\in F_i}w_ne_n\right\|_{\alpha}\ <\ 3. \end{align*} $$
Let X be the completion of
![]() $c_{00}$
under the norm:
$c_{00}$
under the norm:
 $$ \begin{align*} \|(a_n)_n\|\ :=\ \sup_{F_i}\left\{\max_{n}|a_n|, \min F_i\cdot \sum_{n\in F_i} w_n|a_n|\right\}. \end{align*} $$
$$ \begin{align*} \|(a_n)_n\|\ :=\ \sup_{F_i}\left\{\max_{n}|a_n|, \min F_i\cdot \sum_{n\in F_i} w_n|a_n|\right\}. \end{align*} $$
Let
![]() $\mathcal {B}$
be the canonical basis.
$\mathcal {B}$
be the canonical basis.
Claim 4.18 The basis
![]() $\mathcal {B}$
is
$\mathcal {B}$
is
![]() $1$
-unconditional and normalized.
$1$
-unconditional and normalized.
Proof That
![]() $\mathcal {B}$
is
$\mathcal {B}$
is
![]() $1$
-unconditional is obvious. Let us show that
$1$
-unconditional is obvious. Let us show that
![]() $\|e_n\| = 1$
for all
$\|e_n\| = 1$
for all
![]() $n\in \mathbb {N}$
. Fix
$n\in \mathbb {N}$
. Fix
![]() $n\in \mathbb {N}$
. Due to the appearance of
$n\in \mathbb {N}$
. Due to the appearance of
![]() $\|\cdot \|_{\infty }$
,
$\|\cdot \|_{\infty }$
,
![]() $\|e_n\|\geqslant 1$
. Since
$\|e_n\|\geqslant 1$
. Since
![]() $\min F_i \cdot w_n \leqslant 1$
for all
$\min F_i \cdot w_n \leqslant 1$
for all
![]() $i\in \mathbb {N}$
and
$i\in \mathbb {N}$
and
![]() $n\in F_i$
according to Lemma 4.15,
$n\in F_i$
according to Lemma 4.15,
![]() $\|e_n\|\leqslant 1$
. Hence,
$\|e_n\|\leqslant 1$
. Hence,
![]() $\|e_n\| = 1$
.
$\|e_n\| = 1$
.
Claim 4.19 The basis
![]() $\mathcal {B}$
is
$\mathcal {B}$
is
![]() $\mathcal {S}_{\alpha }$
-disjoint democratic. In particular,
$\mathcal {S}_{\alpha }$
-disjoint democratic. In particular,
![]() $\|1_A\| < 3$
for all
$\|1_A\| < 3$
for all
![]() $A\in \mathcal {S}_{\alpha }$
.
$A\in \mathcal {S}_{\alpha }$
.
Proof Choose
![]() $A\in \mathcal {S}_{\alpha }$
. For any
$A\in \mathcal {S}_{\alpha }$
. For any
![]() $F_i$
, we have
$F_i$
, we have
 $$ \begin{align*} \min F_i\cdot \sum_{n\in A\cap F_i}w_n \ \leqslant\ \left\|\min F_i\cdot \sum_{n\in F_i}w_ne_n\right\|_{\alpha}\ < \ 3. \end{align*} $$
$$ \begin{align*} \min F_i\cdot \sum_{n\in A\cap F_i}w_n \ \leqslant\ \left\|\min F_i\cdot \sum_{n\in F_i}w_ne_n\right\|_{\alpha}\ < \ 3. \end{align*} $$
Therefore,
![]() $\|1_A\| < 3$
.
$\|1_A\| < 3$
.
Claim 4.20 The basis
![]() $\mathcal {B}$
is not
$\mathcal {B}$
is not
![]() $\mathcal {S}_{\alpha +1}$
-disjoint democratic.
$\mathcal {S}_{\alpha +1}$
-disjoint democratic.
Proof Choose
![]() $F_i$
, which is a maximal
$F_i$
, which is a maximal
![]() $\mathcal {S}_{\alpha +1}$
-set. Let A be an
$\mathcal {S}_{\alpha +1}$
-set. Let A be an
![]() $\mathcal {S}_{\alpha }$
-set with
$\mathcal {S}_{\alpha }$
-set with
![]() $|F_i| \leqslant |A|$
and
$|F_i| \leqslant |A|$
and
![]() $F_i\sqcup A$
. By how
$F_i\sqcup A$
. By how
![]() $F_i$
’s are defined,
$F_i$
’s are defined,
![]() $\|1_{F_i}\| = \min F_i$
. On the other hand, we have that
$\|1_{F_i}\| = \min F_i$
. On the other hand, we have that
![]() $\|1_A\| < 3$
by Claim 4.19. Since
$\|1_A\| < 3$
by Claim 4.19. Since
![]() $\|1_{F_i}\|/|1_A\|> \min F_i/3 \rightarrow \infty $
as
$\|1_{F_i}\|/|1_A\|> \min F_i/3 \rightarrow \infty $
as
![]() $i\rightarrow \infty $
, the basis
$i\rightarrow \infty $
, the basis
![]() $\mathcal {B}$
is not
$\mathcal {B}$
is not
![]() $\mathcal {S}_{\alpha +1}$
-disjoint democratic.
$\mathcal {S}_{\alpha +1}$
-disjoint democratic.
By Claims 4.18–4.20, our basis
![]() $\mathcal {B}$
is (
$\mathcal {B}$
is (
![]() $\infty $
,
$\infty $
,
![]() $\alpha $
)-quasi-greedy.
$\alpha $
)-quasi-greedy.
5 Proof of Theorem 1.11
Before proceeding to the proof of Theorem 1.11, we isolate the following simple lemma, but omit its straightforward proof.
Lemma 5.1 Let
![]() $\alpha < \omega _1$
and S be a finite set of positive integers with
$\alpha < \omega _1$
and S be a finite set of positive integers with
![]() $\min S \geqslant 2$
. Then there is an
$\min S \geqslant 2$
. Then there is an
![]() $m\in \mathbb {N}$
so that
$m\in \mathbb {N}$
so that
![]() $S \in \mathcal {S}_{\alpha + m}$
.
$S \in \mathcal {S}_{\alpha + m}$
.
Proof of Theorem 1.11
Assume that our basis
![]() $(e_n)$
is greedy. Let
$(e_n)$
is greedy. Let
![]() $m\in \mathbb {N}$
. By Konyagin and Temlyakov’s characterization of greedy bases [Reference Konyagin and Temlyakov15], we know that
$m\in \mathbb {N}$
. By Konyagin and Temlyakov’s characterization of greedy bases [Reference Konyagin and Temlyakov15], we know that
![]() $(e_n)$
is K-unconditional and
$(e_n)$
is K-unconditional and
![]() $\Delta $
-democratic for some
$\Delta $
-democratic for some
![]() $K, \Delta \geqslant 1$
. It follows from the definitions that
$K, \Delta \geqslant 1$
. It follows from the definitions that
![]() $(e_n)$
is K-
$(e_n)$
is K-
![]() $\mathcal {S}_{\alpha + m}$
-unconditional,
$\mathcal {S}_{\alpha + m}$
-unconditional,
![]() $\Delta $
-
$\Delta $
-
![]() $\mathcal {S}_{\alpha + m}$
-disjoint democratic, and K-quasi-greedy. By the proof of Proposition 2.5 and Theorem 2.3,
$\mathcal {S}_{\alpha + m}$
-disjoint democratic, and K-quasi-greedy. By the proof of Proposition 2.5 and Theorem 2.3,
![]() $(e_n)$
is C-
$(e_n)$
is C-
![]() $\mathcal {S}_{\alpha + m}$
-greedy for some
$\mathcal {S}_{\alpha + m}$
-greedy for some
![]() $C = C(K, \Delta )$
.
$C = C(K, \Delta )$
.
Conversely, assume that
![]() $(e_n)$
is C-
$(e_n)$
is C-
![]() $\mathcal {S}_{\alpha + m}$
-greedy for all
$\mathcal {S}_{\alpha + m}$
-greedy for all
![]() $m\in \mathbb {N}$
and some uniform
$m\in \mathbb {N}$
and some uniform
![]() $C\geqslant 1$
. We need to show that
$C\geqslant 1$
. We need to show that
![]() $(e_n)$
is unconditional and disjoint democratic. Let
$(e_n)$
is unconditional and disjoint democratic. Let
![]() ${A\subset \mathbb {N}}$
be a finite set. Write
${A\subset \mathbb {N}}$
be a finite set. Write
![]() $A = (A\cap \{1\})\cup (A\backslash \{1\})$
. By Lemma 5.1, there exists m such that
$A = (A\cap \{1\})\cup (A\backslash \{1\})$
. By Lemma 5.1, there exists m such that
![]() $A\backslash \{1\}\in \mathcal {S}_{\alpha + m}$
. Hence,
$A\backslash \{1\}\in \mathcal {S}_{\alpha + m}$
. Hence,
![]() $\mathcal {S}_{\alpha + m}$
-unconditionality implies that
$\mathcal {S}_{\alpha + m}$
-unconditionality implies that
![]() $\|P_{A\backslash \{1\}}\|\leqslant C+1$
(see Theorem 2.3). Therefore,
$\|P_{A\backslash \{1\}}\|\leqslant C+1$
(see Theorem 2.3). Therefore,
and so
![]() $(e_n)$
is unconditional. Next, we show that
$(e_n)$
is unconditional. Next, we show that
![]() $(e_n)$
is disjoint democratic. Pick finite disjoint sets
$(e_n)$
is disjoint democratic. Pick finite disjoint sets
![]() $A, B\subset \mathbb {N}$
with
$A, B\subset \mathbb {N}$
with
![]() $|A|\leqslant |B|$
. Since
$|A|\leqslant |B|$
. Since
![]() $A\backslash \{1\}\in \mathcal {S}_{\alpha +m}$
for some sufficiently large m and
$A\backslash \{1\}\in \mathcal {S}_{\alpha +m}$
for some sufficiently large m and
![]() $(e_n)$
is C-
$(e_n)$
is C-
![]() $\mathcal {S}_{\alpha + m}$
-disjoint democratic,
$\mathcal {S}_{\alpha + m}$
-disjoint democratic,
![]() $\|1_{A\backslash \{1\}}\|\leqslant C\|1_B\|$
. Furthermore,
$\|1_{A\backslash \{1\}}\|\leqslant C\|1_B\|$
. Furthermore,
We obtain
Hence,
![]() $(e_n)$
is disjoint democratic. This completes our proof.
$(e_n)$
is disjoint democratic. This completes our proof.
Finally, we show that there exists a basis that is
![]() $\mathcal {S}_{\alpha +m}$
-greedy for all
$\mathcal {S}_{\alpha +m}$
-greedy for all
![]() $m\in \mathbb {N}$
but is not greedy. Let
$m\in \mathbb {N}$
but is not greedy. Let
![]() $\beta $
be the smallest limit ordinal that is greater than
$\beta $
be the smallest limit ordinal that is greater than
![]() $\alpha + m$
for all
$\alpha + m$
for all
![]() $m\in \mathbb {N}$
. Consider the canonical basis
$m\in \mathbb {N}$
. Consider the canonical basis
![]() $(e_n)$
of the space
$(e_n)$
of the space
![]() $X_{\beta , \infty }$
in Section 4.2. We have shown that
$X_{\beta , \infty }$
in Section 4.2. We have shown that
![]() $(e_n)$
is
$(e_n)$
is
![]() $\mathcal {S}_{\beta }$
-greedy. By Corollary 1.9,
$\mathcal {S}_{\beta }$
-greedy. By Corollary 1.9,
![]() $(e_n)$
is
$(e_n)$
is
![]() $\mathcal {S}_{\alpha + m}$
-greedy for all m. However, since the basis is not unconditional, it is not greedy.
$\mathcal {S}_{\alpha + m}$
-greedy for all m. However, since the basis is not unconditional, it is not greedy.
6 Future research
In this paper, we show that given a pair
![]() $(\alpha ,\beta ) \in (\omega _1\cup \{\infty \})^2$
, if either
$(\alpha ,\beta ) \in (\omega _1\cup \{\infty \})^2$
, if either
![]() $\alpha $
or
$\alpha $
or
![]() $\beta $
is
$\beta $
is
![]() $\infty $
or if
$\infty $
or if
![]() $(\alpha ,\beta ) = (0,0)$
, there is a Banach space with an
$(\alpha ,\beta ) = (0,0)$
, there is a Banach space with an
![]() $(\alpha , \beta )$
-quasi-greedy basis. The result is sufficient enough to prove Theorem 1.10. A natural extension of our work is whether there is an
$(\alpha , \beta )$
-quasi-greedy basis. The result is sufficient enough to prove Theorem 1.10. A natural extension of our work is whether there is an
![]() $(\alpha ,\beta )$
-quasi-greedy basis for every pair
$(\alpha ,\beta )$
-quasi-greedy basis for every pair
![]() $(\alpha ,\beta ) \in (\omega _1\cup \{\infty \})^2$
.
$(\alpha ,\beta ) \in (\omega _1\cup \{\infty \})^2$
.
Regarding Theorem 1.11, we would like to know whether an
![]() $\mathcal {S}_{\alpha }$
-greedy basis for all countable ordinals
$\mathcal {S}_{\alpha }$
-greedy basis for all countable ordinals
![]() $\alpha $
(with different greedy constants) is greedy. Similarly, must an
$\alpha $
(with different greedy constants) is greedy. Similarly, must an
![]() $\mathcal {S}_{\alpha }$
-unconditional basis for all countable ordinals
$\mathcal {S}_{\alpha }$
-unconditional basis for all countable ordinals
![]() $\alpha $
be unconditional?
$\alpha $
be unconditional?
A Appendix
Lemma A.1 The following hold.
-
(i) If
 $F\in \mathcal {S}_{\alpha }$
for some
$F\in \mathcal {S}_{\alpha }$
for some
 $\alpha $
and
$\alpha $
and
 $\min F = 1$
, then
$\min F = 1$
, then
 $F = \{1\}$
.
$F = \{1\}$
. -
(ii) For all ordinals
 $\alpha \geqslant 0$
,
$\alpha \geqslant 0$
,
 $\mathcal {S}_0\subset \mathcal {S}_{\alpha }$
.
$\mathcal {S}_0\subset \mathcal {S}_{\alpha }$
. -
(iii) For all ordinals
 $\alpha \geqslant 2$
,
$\alpha \geqslant 2$
,
 $\mathcal {S}_2\subset \mathcal {S}_{\alpha }$
.
$\mathcal {S}_2\subset \mathcal {S}_{\alpha }$
.
We omit the straightforward proof of Lemma A.1. For completeness, we include the easy proof of the following lemma.
Lemma A.2 Fix
![]() $\alpha \geqslant 2$
and
$\alpha \geqslant 2$
and
![]() $M\in [\mathbb {N}]$
,
$M\in [\mathbb {N}]$
,
![]() $\min M \geqslant 3$
. Let
$\min M \geqslant 3$
. Let
![]() $\ell _n = \min \alpha (M, n)$
. It holds that
$\ell _n = \min \alpha (M, n)$
. It holds that
![]() $\ell _{n+1}\geqslant 8\ell _n$
for all
$\ell _{n+1}\geqslant 8\ell _n$
for all
![]() $n\geqslant 1$
.
$n\geqslant 1$
.
Proof Let
![]() $L_n = M\backslash \cup _{i=1}^{n-1}\operatorname {\mathrm {supp}}(\alpha (M, i))$
for
$L_n = M\backslash \cup _{i=1}^{n-1}\operatorname {\mathrm {supp}}(\alpha (M, i))$
for
![]() $n\geqslant 1$
. Then
$n\geqslant 1$
. Then
![]() $\min L_n = \ell _n$
for all
$\min L_n = \ell _n$
for all
![]() $n\geqslant 1$
. First, we show that,
$n\geqslant 1$
. First, we show that,
Suppose, for a contradiction, for some n,
Let
![]() $E = \operatorname {\mathrm {supp}} (\alpha (M, n))$
and
$E = \operatorname {\mathrm {supp}} (\alpha (M, n))$
and
![]() $F = \operatorname {\mathrm {supp}} (2(L_n,1))$
. Then
$F = \operatorname {\mathrm {supp}} (2(L_n,1))$
. Then
![]() $E\subsetneq F$
. Since
$E\subsetneq F$
. Since
![]() $F\in \mathcal {S}_2$
,
$F\in \mathcal {S}_2$
,
![]() $F\in \mathcal {S}_{\alpha }$
according to Lemma A.1. That
$F\in \mathcal {S}_{\alpha }$
according to Lemma A.1. That
![]() $E\subsetneq F$
and
$E\subsetneq F$
and
![]() $F\in \mathcal {S}_{\alpha }$
contradict that E is a maximal
$F\in \mathcal {S}_{\alpha }$
contradict that E is a maximal
![]() $\mathcal {S}_{\alpha }$
-set. Therefore, for all
$\mathcal {S}_{\alpha }$
-set. Therefore, for all
![]() $n\geqslant 1$
, (A.1) holds.
$n\geqslant 1$
, (A.1) holds.
We have for all
![]() $n\geqslant 1$
,
$n\geqslant 1$
,
 $$ \begin{align*} \frac{\ell_{n+1}}{\ell_n}\ \geqslant\ \frac{\max\operatorname{\mathrm{supp}} (\alpha(M, n))+1}{\ell_n}\ \geqslant\ \frac{\max\operatorname{\mathrm{supp}} (2(L_n, 1))+1}{\ell_n}\ \geqslant\ \frac{2^{\ell_n} \ell_n}{\ell_n}\ \geqslant \ 8. \end{align*} $$
$$ \begin{align*} \frac{\ell_{n+1}}{\ell_n}\ \geqslant\ \frac{\max\operatorname{\mathrm{supp}} (\alpha(M, n))+1}{\ell_n}\ \geqslant\ \frac{\max\operatorname{\mathrm{supp}} (2(L_n, 1))+1}{\ell_n}\ \geqslant\ \frac{2^{\ell_n} \ell_n}{\ell_n}\ \geqslant \ 8. \end{align*} $$
This completes our proof.