Hostname: page-component-76fb5796d-wq484 Total loading time: 0 Render date: 2024-04-26T09:09:39.064Z Has data issue: false hasContentIssue false
  • English
  • Français

Singular boundary conditions for Sturm–Liouville operators via perturbation theory

Part of: Boundary value problems Ordinary differential operators Stability theory General theory of linear operators

Published online by Cambridge University Press:  23 June 2022

Michael Bush Open the ORCID record for Michael Bush [Opens in a new window] ,
Dale Frymark Open the ORCID record for Dale Frymark [Opens in a new window]  and
Constanze Liaw
Michael Bush
Affiliation:
Department of Mathematical Sciences, University of Delaware, 501 Ewing Hall, Newark, DE 19716, USA e-mail: mikebush@udel.edu liaw@udel.edu
Dale Frymark*
Affiliation:
Department of Theoretical Physics, Nuclear Physics Institute, Czech Academy of Sciences, Řež 25068, Czech Republic
Constanze Liaw
Affiliation:
Department of Mathematical Sciences, University of Delaware, 501 Ewing Hall, Newark, DE 19716, USA e-mail: mikebush@udel.edu liaw@udel.edu Center for Astrophysics, Space Physics & Engineering Research (CASPER), Baylor University, One Bear Place #97328, Waco, TX 76798, USA e-mail: liaw@udel.edu
*
e-mail: frymark@ujf.cas.cz
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that all self-adjoint extensions of semibounded Sturm–Liouville operators with limit-circle endpoint(s) can be obtained via an additive singular form-bounded self-adjoint perturbation of rank equal to the deficiency indices, say 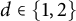$d\in \{1,2\}$. This characterization generalizes the well-known analog for semibounded Sturm–Liouville operators with regular endpoints. Explicitly, every self-adjoint extension of the minimal operator can be written as

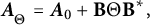$$ \begin{align*} \boldsymbol{A}_{ {}_{\scriptstyle \Theta}}=\boldsymbol{A}_0+\mathbf{B}\Theta\mathbf{B}^*, \end{align*} $$
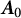where $\boldsymbol {A}_0$ is a distinguished self-adjoint extension and $\Theta $ is a self-adjoint linear relation in 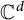$\mathbb {C}^d$. The perturbation is singular in the sense that it does not belong to the underlying Hilbert space but is form-bounded with respect to 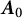$\boldsymbol {A}_0$, i.e., it belongs to 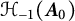$\mathcal {H}_{-1}(\boldsymbol {A}_0)$, with possible “infinite coupling.” A boundary triple and compatible boundary pair for the symmetric operator are constructed to ensure that the perturbation is well defined and self-adjoint extensions are in a one-to-one correspondence with self-adjoint relations $\Theta $.

The merging of boundary triples with perturbation theory provides a more holistic view of the operator’s matrix-valued spectral measures: identifying not just the location of the spectrum, but also certain directional information.

As an example, self-adjoint extensions of the classical Jacobi differential equation (which has two limit-circle endpoints) are obtained, and their spectra are analyzed with tools both from the theory of boundary triples and perturbation theory.

Keywords

Self-adjoint perturbationSturm–Liouvilleself-adjoint extensionspectral theoryboundary tripleboundary pairsingular boundary conditionssingular perturbation

MSC classification

Primary: 47A55: Perturbation theory
Secondary: 34D15: Singular perturbations 34B20: Weyl theory and its generalizations 34B24: Sturm-Liouville theory 34L10: Eigenfunctions, eigenfunction expansions, completeness of eigenfunctions
Type
Article
Information
Canadian Journal of Mathematics , Volume 75 , Issue 4 , August 2023 , pp. 1110 - 1146
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

M. Bush and C. Liaw were partially supported by the National Science Foundation Grant No. DMS-1802682. D. Frymark was partially supported by the Swedish Foundation for Strategic Research under Grant No. AM13-0011. Since August 2020, C. Liaw has been serving as a Program Director in the Division of Mathematical Sciences at the National Science Foundation (NSF), USA, and as a component of this position, she received support from NSF for research, which included work on this paper. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the NSF.

References

Akhiezer, N. and Glazman, I., Theory of linear operators in Hilbert space, Dover Publications, New York, 1993.Google Scholar
Albeverio, S. and Kurasov, P., Singular perturbations of differential operators, London Mathematical Society Lecture Note Series, 271, Cambridge University Press, Cambridge, 2000.CrossRefGoogle Scholar
Aleksandrov, A. B., Multiplicity of boundary values of inner functions . Izv. Akad. Nauk Armyan. SSR Ser. Math. 22(1987), no. 5, 490–503, 515.Google Scholar
Arlinskii, Y., Maximal sectorial extensions and closed forms associated with them . Ukr. Math. J. 48(1996), 723–739.CrossRefGoogle Scholar
Aronszajn, N., On a problem of Weyl in the theory of singular Sturm–Liouville equations . Amer. J. Math. 79(1957), 597–610.CrossRefGoogle Scholar
Bailey, P., Everitt, W., and Zettl, A., Algorithm 810: the SLEIGN2 Sturm–Liouville code . ACM Trans. Math. Software 27(2001), 143—192.CrossRefGoogle Scholar
Behrndt, J., Hassi, S., and de Snoo, H., Boundary value problems, Weyl functions, and differential operators, Monographs in Mathematics, 108, Birkhäuser, Cham, Switzerland, 2020.CrossRefGoogle Scholar
Bochner, S., Über Sturm–Liouvillesche Polynomsysteme . Math. Z. 29(1929), 730–736.CrossRefGoogle Scholar
Brown, R. and Hinton, D., Relative form boundedness and compactness for a second-order differential operator . J. Comput. Appl. Math. 171(2004), 123–140.CrossRefGoogle Scholar
Bruk, V., A certain class of boundary value problems with a spectral parameter in the boundary condition . Mat. Sb. 100(1976), 210–216 (in Russian) [Sb. Math. 29(1976), 186–192].Google Scholar
Bulla, W. and Gesztesy, F., Deficiency indices and singular boundary conditions in quantum mechanics . J. Math. Phys. 26(1985), no. 10, 2520–2528.CrossRefGoogle Scholar
Calkin, J., General self-adjoint boundary conditions for certain partial differential operators . Proc. Natl. Acad. Sci. USA 25(1939), 201–206.CrossRefGoogle ScholarPubMed
Derkach, V. and Malamud, M., On the Weyl function and Hermitian operators with gaps . Soviet Math. Dokl. 35(1987), 393–398 (in Russian) [Doklady Akad. Nauk SSSR 293(1987), 1041–1046].Google Scholar
Derkach, V. and Malamud, M., Generalized resolvents and the boundary value problems for Hermitian operators with gaps . J. Funct. Anal. 95(1991), 1–95.CrossRefGoogle Scholar
Dijksma, A., Kurasov, P., and Shondin, Y., High order singular rank-one perturbations of a positive operator . Integral Equations Operator Theory 53(2005), 209–245.CrossRefGoogle Scholar
Donoghue, W., On the perturbation of spectra . Comm. Pure Appl. Math. 18(1965), 559–579.CrossRefGoogle Scholar
Dunford, N. and Schwartz, J., Linear operators, part II, Wiley Classics Library, New York, 1988.Google Scholar
Eckhardt, J., Gesztesy, F., Nichols, R., and Teschl, G., Weyl–Titchmarsh theory for Sturm–Liouville operators with distributional potentials . Opuscula Math. 33(2013), 467–563.CrossRefGoogle Scholar
Everitt, W., A catalogue of Sturm–Liouville differential equations . In: Sturm–Liouville theory: past and present, Birkhäuser Verlag, Basel, Switzerland, 2001, pp. 271–331.Google Scholar
Everitt, W. and Kalf, H., The Bessel differential equation and the Hankel transform . J. Comput. Appl. Math. 208(2007), 3–19.CrossRefGoogle Scholar
Fleeman, M., Frymark, D., and Liaw, C., Boundary conditions associated with the general left-definite theory for differential operators . J. Approx. Theory 239(2019), 1–28.CrossRefGoogle Scholar
Frymark, D., Boundary triples and Weyl m-functions for powers of the Jacobi differential operator . J. Differential Equations 269(2020), 7931–7974.CrossRefGoogle Scholar
Frymark, D. and Liaw, C., Properties and decompositions of domains for powers of the Jacobi differential operator . J. Math. Anal. Appl. 489(2020), 124–155.CrossRefGoogle Scholar
Frymark, D. and Liaw, C., Spectral analysis, model theory and applications of finite-rank perturbations . In: Invited contribution accepted to proceedings of IWOTA 2018: operator theory, operator algebras and noncommutative topology (Ronald G. Douglas memorial volume), Operator Theory: Advances and Applications, Birkhäuser Verlag, Cham, 2020.Google Scholar
Fulton, C., Parametrizations of Titchmarsh’s m $\left(\unicode{x3bb} \right)$ -functions in the limit circle case . Trans. Amer. Math. Soc. 229(1977), 51–63.Google Scholar
Gesztesy, F., Littlejohn, L., and Nichols, R., On self-adjoint boundary conditions for singular Sturm–Liouville operators bounded from below , J. Differential Equations 269 (2020), no. 9, 6448–6491.CrossRefGoogle Scholar
Gesztesy, F. and Simon, B., Rank-one perturbations at infinite coupling . J. Funct. Anal. 128(1995), 245–252.CrossRefGoogle Scholar
Gesztesy, F. and Tsekanovskii, E., On matrix-valued Herglotz functions . Math. Nachr. 218(2000), 61–138.3.0.CO;2-D>CrossRefGoogle Scholar
Gesztesy, F. and Zinchenko, M., On spectral theory for Schrödinger operators with strongly singular potentials . Math. Nachr. 279(2006), 1041–1082.CrossRefGoogle Scholar
Gesztesy, F. and Zinchenko, M., Sturm–Liouville operators, their spectral theory, and some applications, in preparation.Google Scholar
Gorbachuk, V. and Gorbachuk, M., Boundary value problems for operator differential equations, Naukova Dumka, Kiev, 1984 (in Russian) [Kluwer, 1991].Google Scholar
Ismail, M., Classical and quantum orthogonal polynomials in one variable, Encyclopedia of Mathematics and Its Applications, 98, Cambridge University Press, Cambridge, 2005.CrossRefGoogle Scholar
Kochubei, A., On extensions of symmetric operators and symmetric binary relations . Mat. Zametki 17(1975), 41–48 (in Russian) [Math. Notes 17(1975), 25–28].Google Scholar
Krall, A., Hilbert space, boundary value problems and orthogonal polynomials , Birkhäuser Verlag, Basel, Switzerland, 2002.CrossRefGoogle Scholar
Krein, S. and Petunin, I., Scales of Banach spaces . Russ. Math. Surv. 21(1966), 85–159.CrossRefGoogle Scholar
Kurasov, P., Distribution theory for discontinuous test functions and differential operators with generalized coefficients . J. Math. Anal. Appl. 201(1996), 297–323.CrossRefGoogle Scholar
Kurasov, P., ${\mathbf{\mathcal{H}}}_{-n}$ -perturbations of self-adjoint operators and Krein’s resolvent formula . Integral Equations Operator Theory 45(2003), 437–460.CrossRefGoogle Scholar
Kurasov, P. and Luger, A., An operator theoretic interpretation of the generalized Titchmarsh–Weyl coefficient for a singular Sturm–Liouville problem . Math. Phys. Anal. Geom. 14(2011), no. 2, 115–151.CrossRefGoogle Scholar
Liaw, C. and Treil, S., Rank-one perturbations and singular integral operators . J. Funct. Anal. 257(2009), no. 6, 1947–1975.CrossRefGoogle Scholar
Liaw, C. and Treil, S., Singular integrals, rank-one perturbations and Clark model in general situation. In: Pereyra, M. C., Marcantognini, S., Stokolos, A., and Urbina, W. (eds.), Harmonic analysis, partial differential equations, complex analysis, Banach spaces, and operator theory (volume 2). Celebrating Cora Sadosky’s life. Association for Women in Mathematics Series, 5, Springer, Cham, Switzerland, 2017, pp. 86–132.Google Scholar
Liaw, C. and Treil, S., Matrix measures and finite rank perturbations of self-adjoint operators . J. Spectr. Theory 10(2020), 1173–1210.CrossRefGoogle Scholar
Littlejohn, L. and Wellman, R., A general left-definite theory for certain self-adjoint operators with applications to differential equations . J. Differential Equations 181(2002), 280–339.CrossRefGoogle Scholar
Lyantse, V. and Storozh, O., Methods of the theory of unbounded operators, Naukova Dumka, Kiev, 1983.Google Scholar
Marletta, M. and Zettl, A., The Friedrichs extension of singular differential operators . J. Differential Equations 160(2000), 404–421.CrossRefGoogle Scholar
Naimark, M., Linear differential operators, parts I and II, Frederick Ungar Publishing Co., New York, 1972.Google Scholar
Niessen, H. and Zettl, A., Singular Sturm–Liouville problems: the Friedrichs extension and comparison of eigenvalues . Proc. Lond. Math. Soc. 64(1992), 545–578.CrossRefGoogle Scholar
Poltoratskiĭ, A. G., Boundary behavior of pseudocontinuable functions . Algebra i Analiz 5(1993), no. 2, 189–210.Google Scholar
Simon, B., Spectral analysis of rank one perturbations and applications . In: Mathematical quantum theory II. Schrödinger operators (Vancouver, BC, 1993), CRM Proceedings & Lecture Notes, 8, American Mathematical Society, Providence, RI, 1995, pp. 109–149.CrossRefGoogle Scholar
Simon, B., Trace ideals and their applications, 2nd ed., American Mathematical Society, Providence, RI, 2005.Google Scholar
Simon, B. and Wolff, T., Singular continuous spectrum under rank-one perturbations and localization for random Hamiltonians . Comm. Pure Appl. Math. 39(1986), 75–90.CrossRefGoogle Scholar
Szegö, G., Orthogonal polynomials, 4th ed., American Mathematical Society, Providence, RI, 1975.Google Scholar
Titchmarsh, E., Eigenfunction expansions associated with second-order differential equations: I, Clarendon Press, Oxford, 1962.CrossRefGoogle Scholar
Wang, A. and Zettl, A., Ordinary differential operators, Mathematical Surveys and Monographs, 245, American Mathematical Society, Providence, RI, 2019.CrossRefGoogle Scholar
Weyl, H., Über gewöhnliche Differentialgleichungen mit Singularitäten und die zugehörigen Entwicklungen willkürlicher Funktionen . Math. Ann. 68(1910), 220–269.CrossRefGoogle Scholar
Zettl, A., Sturm–Liouville theory, Mathematical Surveys and Monographs, 121, American Mathematical Society, Providence, RI, 2005.Google Scholar