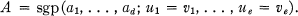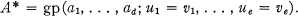Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Dlab, Vlastimil
and
Neumann, B. H.
1969.
Semigroups with few endomorphisms.
Journal of the Australian Mathematical Society,
Vol. 10,
Issue. 1-2,
p.
162.
Cannon, John J.
1971.
Computing the ideal structure of finite semigroups.
Numerische Mathematik,
Vol. 18,
Issue. 3,
p.
254.
Wells, Charles
1976.
Some Applications of the Wreath Product Construction.
The American Mathematical Monthly,
Vol. 83,
Issue. 5,
p.
317.
Jürgensen, H.
1977.
Computers in semigroups.
Semigroup Forum,
Vol. 15,
Issue. 1,
p.
1.
Jura, Andrzej
1978.
Coset Enumeration in a Finitely Presented Semigroup.
Canadian Mathematical Bulletin,
Vol. 21,
Issue. 1,
p.
37.
Jürgensen, H.
1979.
Transformationendarstellungen endlicher abstrakt präsentierter Halbgruppen.
Computing,
Vol. 21,
Issue. 4,
p.
333.
Campbell, Colin M.
Robertson, Edmund F.
and
Thomas, Richard M.
1993.
Applications of Fibonacci Numbers.
p.
77.
Robertson, Edmund F.
and
Ünlü, Yusuf
1993.
On semigroup presentations.
Proceedings of the Edinburgh Mathematical Society,
Vol. 36,
Issue. 1,
p.
55.
Campbell, C. M.
Robertson, E. F.
and
Thomas, R. M.
1993.
On a class of semigroups with symmetric presentations.
Semigroup Forum,
Vol. 46,
Issue. 1,
p.
286.
Campbell, C. M.
Robertson, E. F.
Ruškuc, N.
and
Thomas, R. M.
1995.
Reidemeister-Schreier type rewriting for semigroups.
Semigroup Forum,
Vol. 51,
Issue. 1,
p.
47.
Campbell, C. M.
Robertson, E. F.
Ruškuc, N.
Thomas, R. M.
and
Ünlü, Y.
1995.
Certain one-relator products of semigroups.
Communications in Algebra,
Vol. 23,
Issue. 14,
p.
5207.
Ruškuc, N.
1995.
Matrix semigroups—generators and relations.
Semigroup Forum,
Vol. 51,
Issue. 1,
p.
319.
Umar, Abdullahi
1997.
Some remarks about fibonacci groups and semigroups.
Communications in Algebra,
Vol. 25,
Issue. 12,
p.
3973.
Ruškuc, N.
and
Thomas, R.M.
1998.
Syntactic and Rees Indices of Subsemigroups.
Journal of Algebra,
Vol. 205,
Issue. 2,
p.
435.
Ruškuc, N.
2000.
Algorithmic Problems in Groups and Semigroups.
p.
235.
Praeger, Cheryl E.
2010.
Bernhard Hermann Neumann AC. 15 October 1909 — 21 October 2002.
Biographical Memoirs of Fellows of the Royal Society,
Vol. 56,
Issue. ,
p.
285.
Jones, Sam A.M.
and
Thomas, Richard M.
2018.
Word problems of groups: Formal languages, characterizations and decidability.
Theoretical Computer Science,
Vol. 750,
Issue. ,
p.
2.
Shneerson, L. M.
and
Easdown, D.
2019.
On finite presentations of inverse semigroups with zero having polynomial growth.
Semigroup Forum,
Vol. 99,
Issue. 2,
p.
391.
Nyberg-Brodda, Carl-Fredrik
2022.
On the word problem for special monoids.
Semigroup Forum,
Vol. 105,
Issue. 1,
p.
295.
Nyberg-Brodda, Carl-Fredrik
2023.
Non-finitely generated maximal subgroups of context-free monoids.
Journal of Algebra,
Vol. 616,
Issue. ,
p.
227.