Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-02T20:09:54.095Z Has data issue: false hasContentIssue false
  • English
  • Français

A Spectral Sequence for Cohomotopy

Published online by Cambridge University Press:  20 November 2018

Benson Samuel Brown
Benson Samuel Brown*
Affiliation:
Sir George Williams University, Montreal, Quebec
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a prime number p let 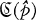be the class of finite abelian groups whose orders are prime to p. For a finitely generated abelian group G, let Gp be the sum of the free and p-primary components of G. Our aim in this paper is to prove the following theorem.

Theorem. Suppose that

(i) Hi(X;Z) = 0 for i > k,

(ii) 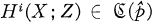for i > k – d

Then there exists a spectral sequence with

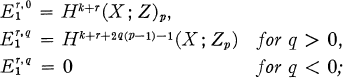
and the differential 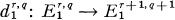is given by

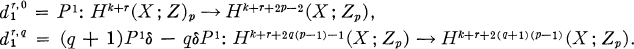
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 21 , 1969 , pp. 712 - 729
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Adams, J. F., Stable homotopy theory. Notes by Vasquez, A. T., University of California, Berkeley, 1961; lecture notes in mathematics, no. 3 (Springer-Verlag, Berlin, 1964).Google Scholar
2. Adem, J., The relations on Steenrod powers of cohomology classes, ﹛Algebraic geometry and topology), A symposium in honor of S. Lefschetz, pp. 191–238 (Princeton Univ. Press, Princeton, N.J., 1957).Google Scholar
3. Barcus, W. D. and Meyer, J.-P., The suspension of a loop space, Amer. J. Math. 80 (1958), 895–920.Google Scholar
4. Brown, B. S., The mod <E suspension theorem, Can. J. Math. 21 (1969), 684–701.Google Scholar
5. Brown, B. S., A first approximation to ﹛X, Y), Can. J. Math. 21 (1969), 702–711.Google Scholar
6. Cartan, H., Algebres d’ Eilenberg-MacLane et homotopie, Séminaire Henri Cartan, 1954-1955 (Secrétariat mathématique, 1956).Google Scholar
7. Eckmann, B. and Hilton, P. J., Décomposition homologique d'un polyèdre simplement connexe, C. R. Acad. Sci. Paris 248 (1959), 2054–2056.Google Scholar
8. Eilenberg, S. and MacLane, S., Relations between homology and homotopy groups of spaces, Ann. of Math. (2) 46 (1945), 480–509.Google Scholar
9. Hu, S.-T., Homotopy theory, Pure and Applied Mathematics, Vol. VIII (Academic Press, New York, 1959).Google Scholar
10. Moore, J. C., On homotopy groups of spaces with a single non-vanishing homology group, Ann. of Math. (2) 59 (1954), 549–557.Google Scholar
11. Serre, J.-P., Homologie singulière des espaces fibres. Applications, Ann. of Math. (2) 54 (1951), 425–505.Google Scholar
12. Serre, J.-P., Groupes d'homotopie et classes de groupes abéliens, Ann. of Math. (2) 58 (1953), 258–294.Google Scholar
13. Serre, J.-P., Cohomologie modulo 2 des complexes d'Eilenberg-MacLane, Comment. Math. Helv. 27 (1953), 198–232.Google Scholar
14. Spanier, E. H., Duality and the suspension category, International Symposium of Algebraic Topology, Symposium Internacional de Topologia Algebrica, 1956 (Universidad Nacional Atonoma de Mexico, UNESCO, 1958).Google Scholar
15. Thomas, P. E., “A spectral sequence for X-theory”, Appendix m Lectures on K(X) by Bott, R. H., Harvard University, 1962.Google Scholar
16. Toda, H., p-primary components of homotopy groups. II. mod p Hopf invariant, Mem. Coll. Sci. Univ. Kyoto Ser. A Math. 31 (1958), 143–160.Google Scholar
17. Toda, H., p-primary components of homotopy groups. IV. Compositions and toric constructions, Mem. Coll. Sci. Univ. Kyoto Ser. A Math. 82 (1959), 297–332.Google Scholar