This paper starts by introducing a bi-periodic summation formula for automorphic forms on a group 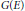$G\left( E \right)$, with periods by a subgroup 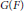$G\left( F \right)$, where 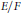$E/F$ is a quadratic extension of number fields. The split case, where 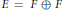$E=F\oplus F$, is that of the standard trace formula. Then it introduces a notion of stable bi-conjugacy, and stabilizes the geometric side of the bi-period summation formula. Thus weighted sums in the stable bi-conjugacy class are expressed in terms of stable bi-orbital integrals. These stable integrals are on the same endoscopic groups 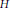$H$ which occur in the case of standard conjugacy.

The spectral side of the bi-period summation formula involves periods, namely integrals over the group of $F$-adele points of $G$, of cusp forms on the group of $E$-adele points on the group $G$. Our stabilization suggests that such cusp forms—with non vanishing periods—and the resulting bi-period distributions associated to “periodic” automorphic forms, are related to analogous bi-period distributions associated to “periodic” automorphic forms on the endoscopic symmetric spaces 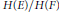$H\left( E \right)/H\left( F \right)$. This offers a sharpening of the theory of liftings, where periods play a key role.

The stabilization depends on the “fundamental lemma”, which conjectures that the unit elements of the Hecke algebras on $G$ and 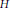$H$ have matching orbital integrals. Even in stating this conjecture, one needs to introduce a “transfer factor”. A generalization of the standard transfer factor to the bi-periodic case is introduced. The generalization depends on a new definition of the factors even in the standard case.

Finally, the fundamental lemma is verified for 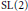$\text{SL}\left( 2 \right)$.