Hostname: page-component-848d4c4894-4hhp2 Total loading time: 0 Render date: 2024-06-08T12:39:06.168Z Has data issue: false hasContentIssue false
  • English
  • Français

The Structure of Continuous {0, 1}-Valued Functions on a Topological Product

Published online by Cambridge University Press:  20 November 2018

S. Broverman
S. Broverman*
Affiliation:
University of Manitoba Winnipeg, Manitoba
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we investigate the question of which continuous ﹛0, 1﹜-valued functions on a product space 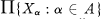admit continuous extensions to 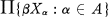where βXα is the Stone-Čech compactification of Xa and ﹛0, 1﹜ denotes the two point discrete space. This problem is clearly equivalent to determining which clopen subsets of have clopen closures in .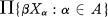

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 28 , Issue 3 , 01 June 1976 , pp. 553 - 559
Copyright
Copyright © Canadian Mathematical Society 1976

References

1. Banaschewski, B., Uber nulldimensionale Raiime, Math. Nachr. 13 (1955), 129–140.Google Scholar
2. Bourbaki, N., General topology (Addison-Wesley, Reading, Mass. 1966).Google Scholar
3. Broverman, S., The topological extension of a product, to appear, Can. Math. Bull.Google Scholar
4. Comfort, W. W., A non-pseudocompact product space whose finite subproducts are pseudocompact, Math. Ann. 170 (1967), 41–44.Google Scholar
5. Comfort, W. W. and Hager, A. W., The projection mapping and other continuous functions on a product space, Math. Scand. 28 (1971), 77–90.Google Scholar
6. Comfort, W. W. and Negrepontis, S., Extending continuous functions on X X Y to subsets of 0X X j8F, Fund. Math. 59 (1966), 1–12.Google Scholar
7. Gillman, L. and Jerison, M., Rings of continuous functions (Van Nostrand, Princeton, 1960).Google Scholar
8. Glicksberg, I., Stone-Cech compactifications of products, Trans. Amer. Math. Soc. 90 (1959), 369–382.Google Scholar