Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Torchinsky, Alberto
2022.
A Modern View of the Riemann Integral.
Vol. 2309,
Issue. ,
p.
95.
Torchinsky, Alberto
2022.
A Modern View of the Riemann Integral.
Vol. 2309,
Issue. ,
p.
1.

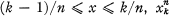 an arbitrarily chosen point of X
an arbitrarily chosen point of X