Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T12:19:09.947Z Has data issue: false hasContentIssue false
  • English
  • Français

A Tauberian Theorem for the General Euler-Borel Summability Method

Published online by Cambridge University Press:  20 November 2018

Laying Tam
Laying Tam*
Affiliation:
The Ohio State University, ColumbusOhio
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Our main result is a Tauberian theorem for the general Euler-Borel summability method. Examples of the method include the discrete Borel, Euler, Meyer- Kônig, Taylor and Karamata methods. Every function/ analytic on the closed unit disk and satisfying some general conditions generates such a method, denoted by (£,ƒ). For instance the function ƒ(z) = exp(z — 1) generates the discrete Borel method. To each such function ƒ corresponds an even positive integer p = p(f).We show that if a sequence (sn)is summable (E,f)and as n→ ∞ m > n, (m— n)n-p(f)→0, then (sn)is convergent. If the Maclaurin coefficients of/ are nonnegative, then p(f) =2. In this case we may replace the condition 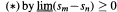. This generalizes the Tauberian theorems for Borel summability due to Hardy and Littlewood, and R. Schmidt. We have also found new examples of the method and proved that the exponent —p(f)in the Tauberian condition (*) is the best possible.

Keywords

Primary: 40E0540G0540G10
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 44 , Issue 5 , 01 October 1992 , pp. 1100 - 1120
Copyright
Copyright © Canadian Mathematical Society 1992

References

1. BajSanski, B., Sur une classe générale de procédés de sommations du type d ‘ Euler-Borel, Acad. Serbe Sci. Publi. Insti. Math. 10(1956), 131–152.Google Scholar
2. Bingham, N.H., On Euler and Borel summability, J. London Math. Soc. (2) 29(1984), 141–146.Google Scholar
3. Bingham, N.H., Tauberian theorems for summability methods of random-walk type, J. London Math. Soc. (2) 30(1984), 281–287.Google Scholar
4. Bingham, N.H., Tauberian theorems for Jakimovski and Karamata-Stiding methods, Mathematika 35(1988), 216–224.Google Scholar
5. Clunie, J. and Vermes, P., Regular Sonnenschein type summability methods, Acad. Roy. Belg. Bull. CI. Sci. (5) 45(1959), 930–954.Google Scholar
6. Fridy, J.A. and Powell, R.E., Tauberian theorems for matrices generated by analytic functions, Pacific J. Math. 192(1981), 79–85.Google Scholar
7. Girard, D.M., The asymptotic behavior of norms of powers of absolutely convergent Fourier series, Pacific J. Math. 37(1971), 357–381.Google Scholar
8. Hardy, G.H., Divergent series, Oxford University Press, 1949.Google Scholar
9. Kwee, B., An improvement on a theorem of Hardy and Littlewood, J. London Math. Soc. (2) 1 28(1983), 93–102.Google Scholar
10. Newman, D., Homomorphisms of ℓ+ , Amer. J. Math. 91(1969), 37–46.Google Scholar
11. Sitaraman, Y., On Tauberian theorems for the Sα-method of summability, Math. Z 95(1967), 34–49.Google Scholar
12. Tenenbaum, G., Sur la procédé de sommation de Borel et la répartition du nombre des facteurs premiers des entiers, Enseignement Math. 26(1980), 225–245.Google Scholar
13. Vijayaraghavan, T., A theorem concerning the summability of series by BoreVs method, Proc. London Math. Soc. (2) 27(1928), 316–326.Google Scholar
14. Zeller, K. and Beekman, W., Théorie der Limitierungsverfahren, Springer Verlag, 1970.Google Scholar