Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T13:25:58.225Z Has data issue: false hasContentIssue false
  • English
  • Français

Three Topological Properties from Noetherian Rings

Published online by Cambridge University Press:  20 November 2018

Jon L. Johnson
Jon L. Johnson*
Affiliation:
Elmhurst College, Elmhurst, Illinois
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The purpose of this paper is to study three concepts that deal with the topologies on ideals of commutative integral domains. We call a domain R prime-injective if for each torsion free R-module M, and all non-zero prime ideals

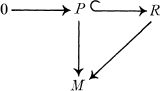
commutes implies that M is injective. From [6, Theorem 1 and the technique of Example 6] this is equivalent to all non-zero ideals of R being open in the topology defined by finite products of non-zero prime ideals as a base of neighborhoods around zero.

A domain is strongly prime-injective if for each (torsion theory) topology and for ϕ the set of primes in , ϕ-injective implies -injective for torsion free modules (see [6, 8] for notation). As in the prime-injective case, this is equivalent to being the topology generated by ϕ for all topologies .

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 34 , Issue 3 , 01 June 1982 , pp. 525 - 534
Copyright
Copyright © Canadian Mathematical Society 1982

References

1. Anderson, D. D., The Krull intersection theorem, Pacific J. Math. 57 (1975), 11–14.Google Scholar
2. Matijevic, J. and Nichols, W., The Krull intersection theorem II, Pacific J. Math. (1976), 15–22.Google Scholar
3. Armeanu, I., On a class of Laskerian rings, Rev. Roum. Math. Pures et Appl. 22 (1977), 1033–1036.Google Scholar
4. Beck, I., Σ-injective modules, J. of Alg. 21 (1972), 232–249.Google Scholar
5. Gilmer, R., Multiplicative ideal theory (Marcel Dekker, New York, 1972.Google Scholar
6. Johnson, J. L., Modules infective with respect to primes, Comm. in Alg. 7 (1979), 327–332.Google Scholar
7. Kaplansky, I., Commutative rings (Allyn and Bacon, Boston, Mass., 1970.Google Scholar
8. Stenstrom, B., Rings and modules of quotients, L.N.M. 237 (Springer-Verlag, 1971.Google Scholar
9. Nagata, M., Local rings (Interscience, New York, 1962.Google Scholar
10. Matijevic, J., Some topics in graded rings, Thesis, University of Chicago (1973).Google Scholar
11. Ohm, J. and Pendleton, R. L., Rings with Noetherian spectrum, Duke J. Math. 35 Google Scholar