Hostname: page-component-848d4c4894-wg55d Total loading time: 0 Render date: 2024-06-09T01:16:18.002Z Has data issue: false hasContentIssue false
  • English
  • Français

Transfer of Plancherel Measures for Unitary Supercuspidal Representations between p-adic Inner Forms

Published online by Cambridge University Press:  20 November 2018

Kwangho Choiy
Kwangho Choiy*
Affiliation:
Department of Mathematics, Purdue University, West Lafayette, IN 47907, U.S.A Department of Mathematics, Oklahoma State University, Stillwater, OK 74078-1058, USA. e-mail: kchoiy@math.purdue.edu, kwangho.choiy@okstate.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $F$ be a 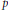$p$-adic field of characteristic 0, and let 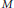$M$ be an $F$-Levi subgroup of a connected reductive $F$-split group such that 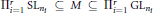$\Pi _{i=1}^{r}\,\text{S}{{\text{L}}_{ni}}\,\subseteq \,M\,\subseteq \,\Pi _{i=1}^{r}\,\text{G}{{\text{L}}_{ni}}$ for positive integers $r$ and ${{n}_{i}}$. We prove that the Plancherel measure for any unitary supercuspidal representation of 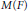$M\left( F \right)$ is identically transferred under the local Jacquet–Langlands type correspondence between 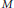$M$ and its $F$-inner forms, assuming a working hypothesis that Plancherel measures are invariant on a certain set. This work extends the result of Muić and Savin (2000) for Siegel Levi subgroups of the groups 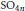$\text{S}{{\text{O}}_{4n}}$ and 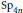$\text{S}{{\text{p}}_{4n}}$ under the local Jacquet–Langlands correspondence. 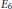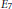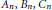It can be applied to a simply connected simple $F$-group of type ${{E}_{6}}$ or ${{E}_{7}}$, and a connected reductive $F$-group of type ${{A}_{n}},\,{{B}_{n}},\,{{C}_{n}}$ or 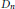${{D}_{n}}$.

Keywords

22E5011F7022E5522E35Plancherel measureinner formlocal to global global argumentcuspidal automorphic representationJacquet-Langlands correspondence
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 66 , Issue 3 , 01 June 2014 , pp. 566 - 595
Copyright
Copyright © Canadian Mathematical Society 2014

References

[1] Arthur, James, Intertwining operators and residues. I. Weighted characters. J. Funct. Anal. 84(1989), 19–84.http://dx.doi.org/10.1016/0022-1236(89)90110-9 Google Scholar
[2] Arthur, James, The endoscopic classification of representations: Orthogonal and symplectic groups. Preprint, 2011.Google Scholar
[3] Arthur, James and Clozel, Laurent, Simple algebras, base change, and the advanced theory of the trace formula. Ann. of Math. Stud. 120, Princeton University Press, Princeton, NJ, 1989.Google Scholar
[4] Badulescu, A. I. and Renard, D., Unitary dual of GL(n) at Archimedean places and global Jacquet–Langlands correspondence. Compositio Math. 146(2010), 1115–1164. http://dx.doi.org/10.1112/S0010437X10004707/ Google Scholar
[5] Ioan Badulescu, Alexandru, Correspondance de Jacquet–Langlands pour les corps locaux de caractćristique non nulle. Ann. Sci. École Norm. Sup. 35(2002), 695–747.Google Scholar
[6] Ioan Badulescu, Alexandru, Alexandru Ioan Badulescu], Global Jacquet–Langlands correspondence, multiplicity one and classification of automorphic representations. With an appendix by Neven Grbac. Invent. Math. 172(2008), 383–438. http://dx.doi.org/10.1007/s00222-007-0104-8 Google Scholar
[7] Borel, A., Automorphic L-functions. In: Automorphic forms, representations and L-functions (Proc. Sympos. Pure Math., Oregon State Univ., Corvallis, Ore., 1977), Part 2, Proc. Sympos. Pure Math. XXXIII, Amer. Math. Soc., Providence, R.I., 1979, 27–61.Google Scholar
[8] Bushnell, Colin J. and Henniart, Guy, The local Langlands conjecture for GL(2). Grundlehren Math. Wiss. 335, Springer-Verlag, Berlin, 2006.Google Scholar
[9] Casselman, W., The unramified principal series of p-adic groups. I. The spherical function. Compositio Math. 40(1980), 387–406.Google Scholar
[10] Choiy, Kwangho, Transfer of Plancherel measures for discrete series representations between p-adic inner forms.With an appendix by Tasho Kaletha. Submitted, 2012.Google Scholar
[11] Cogdell, James W., Kim, Henry H., and Ram Murty, M., Lectures on automorphic L-functions. Fields Inst. Monogr. 20, Amer. Math. Soc., Providence, RI, 2004.Google Scholar
[12] Deligne, P., Kazhdan, D., and Vignćras, M.-F., Reprćsentations des algèbres centrales simples p-adiques. In: Representations of reductive groups over a local field, Travaux en Cours, Hermann, Paris, 1984, 33–117.Google Scholar
[13] Flath, Daniel, A comparison of the automorphic representations of GL(3) and its twisted forms. Pacific J. Math. 97(1981), 373–402. http://dx.doi.org/10.2140/pjm.1981.97.373 Google Scholar
[14] Teck Gan, Wee and Savin, Gordan, Representations of metaplectic groups I: epsilon dichotomy and local Langlands correspondence. Compositio Math. 148(2012), 1655–1694.Google Scholar
[15] Teck Gan, Wee and Takeda, Shuichiro, The local Langlands conjecture for Sp(4). Int. Math. Res. Not. IMRN 2010, 2987–3038.Google Scholar
[16] Teck Gan, Wee, The local Langlands conjecture for GSp(4). Ann. of Math. (2) 173(2011), 1841–1882. ,http://dx.doi.org/10.4007/annals.2011.173.3.12 Google Scholar
[17] Teck Gan, Wee and Tantono, Welly, The local Langlands conjecture for GSp(4) II: the case of innerforms. Preprint, 2012.Google Scholar
[18] Gelbart, S. S. and Knapp, A.W., L-indistinguishability and R groups for the special linear group. Adv. in Math. 43(1982), 101–121. http://dx.doi.org/10.1016/0001-8708(82)90030-5 Google Scholar
[19] Haines, Thomas J. and Rostami, Sean, The Satake isomorphism for special maximal parahoric Hecke algebras. Represent. Theory 14(2010), 264–284. http://dx.doi.org/10.1090/S1088-4165-10-00370-5 Google Scholar
[20] Chandra, Harish, Harmonic analysis on reductive p-adic groups. Notes by G. van Dijk. Lecture Notes in Math. 162, Springer-Verlag, Berlin, 1970.Google Scholar
[21] Chandra, Harish, Harmonic analysis on reductive p-adic groups. In: Harmonic analysis on homogeneous spaces (Proc. Sympos. Pure Math. XXVI, Williams Coll., Williamstown, Mass., 1972), Amer. Math. Soc., Providence, RI, 1973, 167–192.Google Scholar
[22] Chandra, Harish, Harmonic analysis on real reductive groups. III. The Maass–Selberg relations and the Plancherel formula. Ann. of Math. (2) 104(1976), 117–201. http://dx.doi.org/10.2307/1971058 Google Scholar
[23] Chandra, Harish, A submersion principle and its applications. Proc. Indian Acad. Sci. Math. Sci. 90(1981), 95–102. http://dx.doi.org/10.1007/BF02837281 Google Scholar
[24] Henniart, Guy, La conjecture de Langlands locale pour GL(3). Mém. Soc. Math. France (N.S.) (11–12)(1984), 186.Google Scholar
[25] Hiraga, Kaoru and Saito, Hiroshi, On L-packets for inner forms of SL(n). Mem. Amer. Math. Soc. 215(2011), 97.Google Scholar
[26] Jacquet, H. and Langlands, R. P., Automorphic forms on GL(2). Lecture Notes in Math. 114, Springer-Verlag, Berlin, 1970.Google Scholar
[27] David Keys, C. and Shahidim, Freydoon, Artin L-functions and normalization of intertwining operators. Ann. Sci. École Norm. Sup. (4) 21(1988), 67–89.Google Scholar
[28] Kim, Henry H., On local L-functions and normalized intertwining operators. Canad. J. Math. 57(2005), 535–597. http://dx.doi.org/10.4153/CJM-2005-023-x Google Scholar
[29] Knapp, A. W. and Zuckerman, Gregg J., Classification of irreducible tempered representations of semisimple groups. Ann. of Math. (2) 116(1982), 389–455. http://dx.doi.org/10.2307/2007066 Google Scholar
[30] Kottwitz, Robert E., Stable trace formula: elliptic singular terms. Math. Ann. 275(1986), 365–399. http://dx.doi.org/10.1007/BF01458611 Google Scholar
[31] Kottwitz, Robert E., Isocrystals with additional structure. II. Compositio Math. 109(1997), 255–339. http://dx.doi.org/10.1023/A:1000102604688 Google Scholar
[32] Kudla, Stephen S., The local Langlands correspondence: the non-Archimedean case. In: Motives (Seattle,WA, 1991), Proc. Sympos. Pure Math. 55, Amer. Math. Soc., Providence, RI, 1994, 365–391.Google Scholar
[33] Lang, Serge, Algebraic number theory. Graduate Texts in Math. 110, second edition, Springer-Verlag, New York, 1994.Google Scholar
[34] Langlands, Robert P., Euler products. A James K.Whittemore Lecture in Mathematics given at Yale University, 1967, Yale Mathematical Monographs 1, Yale University Press, New Haven, Conn., 1971.Google Scholar
[35] Langlands, Robert P., On the notion of an automorphic representation. a supplement to the preceding paper. In: Automorphic forms, representations and L-functions (Proc. Sympos. Pure Math., Oregon State Univ., Corvallis, Ore., 1977), Part 1, Proc. Sympos. Pure Math. XXXIII, Amer. Math. Soc., Providence, RI, 1979, 203–207.Google Scholar
[36] Langlands, Robert P., On the classification of irreducible representations of real algebraic groups. In: Representation theory and harmonic analysis on semisimple Lie groups, Math. Surveys Monogr. 31, Amer. Math. Soc., Providence, RI, 1989, 101–170.Google Scholar
[37] Muiá, Goran and Savin, Gordan, Complementary series for Hermitian quaternionic groups. Canad. Math. Bull. 43(2000), 90–99. http://dx.doi.org/10.4153/CMB-2000-014-5 Google Scholar
[38] Platonov, Vladimir and Rapinchuk, Andrei, Algebraic groups and number theory. Pure Appl. Math. 139, Academic Press Inc., Boston, MA, 1994.Google Scholar
[39] Rogawski, Jonathan D., Representations of GL(n) and division algebras over a p-adic field. Duke Math. J. 50(1983), 161–196. http://dx.doi.org/10.1215/S0012-7094-83-05006-8 Google Scholar
[40] Satake, I., Classification theory of semi-simple algebraic groups. With an appendix by M. Sugiura, Notes prepared by Doris Schattschneider. Lecture Notes Pure Appl. Math. 3, Marcel Dekker Inc., New York, 1971.Google Scholar
[41] Shahidi, Freydoon, On the Ramanujan conjecture and finiteness of poles for certain L-functions. Ann. of Math. (2) 127(1988), 547–584. http://dx.doi.org/10.2307/2007005 Google Scholar
[42] Shahidi, Freydoon, A proof of Langlands’ conjecture on Plancherel measures; complementary series for p-adic groups. Ann. of Math. (2) 132(1990), 273–330. http://dx.doi.org/10.2307/1971524 Google Scholar
[43] Shahidi, Freydoon, Langlands’ conjecture on Plancherel measures for p-adic groups. In: Harmonic analysis on reductive groups (Brunswick, ME, 1989), Progr. Math. 101, Birkhäuser Boston, Boston, MA, 1991, 277–295.Google Scholar
[44] Woo Shin, Sug, A stable trace formula for Igusa varieties. J. Inst. Math. Jussieu 9(2010), 847–895. http://dx.doi.org/10.1017/S1474748010000046 Google Scholar
[45] Silberger, Allan J., Introduction to harmonic analysis on reductive p-adic groups. Math. Notes 23, Princeton University Press, Princeton, NJ, 1979.Google Scholar
[46] Silberger, Allan J., Special representations of reductive p-adic groups are not integrable. Ann. of Math. (2) 111(1980), 571–587. http://dx.doi.org/10.2307/1971110 Google Scholar
[47] Snowden, Andrew, The Jacquet–Langlands correspondence for GL(2). Ph.D. dissertation, Princeton University, 2009.Google Scholar
[48] Tadić, Marko, Notes on representations of non-Archimedean SL(n). Pacific J. Math. 152(1992), 375–396. http://dx.doi.org/10.2140/pjm.1992.152.375 Google Scholar
[49] Waldspurger, J.-L., La formule de Plancherel pour les groupes p-adiques (d’après Harish-Chandra). J. Inst. Math. Jussieu 2(2003), 235–333. http://dx.doi.org/10.1017/S1474748003000082 Google Scholar