Hostname: page-component-7bb8b95d7b-cx56b Total loading time: 0 Render date: 2024-09-15T11:15:52.705Z Has data issue: false hasContentIssue false
  • English
  • Français

Uniform Approximation by Polynomials with Variable Exponents

Published online by Cambridge University Press:  20 November 2018

Peter B. Borwein
Peter B. Borwein*
Affiliation:
Dalhousie University, Halifax, Nova Scotia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We examine questions related to approximating functions by sums of the form

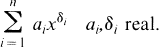
We focus on approximations to functions given by the integral transformation

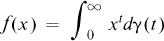
where γ is a positive measure. Approximations to this class of functions (Laplace transforms in the variable — lnx) are particularly well behaved (see Theorem 1). Questions concerning existence, uniqueness and characterization of such approximations have been thoroughly examined in the equivalent setting of exponential sum approximations (see [3], [4], [6] and [9]). Less well studied is the order of convergence of the approximation. This is the problem we address. Part of the motivation for using sums of the form (1), which we shall call Gaussian sums, stems from the observation that all analytic functions with Taylor series expansion having positive coefficients are of the form (2).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 35 , Issue 3 , 01 June 1983 , pp. 547 - 557
Copyright
Copyright © Canadian Mathematical Society 1983

References

1. Baker, G. A. Jr. and Graves-Morris, P., Padé approximatifs, Vol. 1 (Addison-Wesley, Reading, Mass., 1981).Google Scholar
2. Borwein, P., Rational approximations to Stieltjes transforms, Math. Scandinavica (To appear).CrossRefGoogle Scholar
3. Braess, D., Chebyshev approximation by γ-polynomials, J. Approx. Theory 9 (1973), 20–43.Google Scholar
4. Kammler, D. W., Chebyshev approximation of completely monotonie functions by sums of exponentials, SI AM J. Numer. Anal. 75 (1976), 761–774.Google Scholar
5. Karlin, S., Total positivity, Vol. 1 (Stanford Univ. Press, Stanford, California, 1968).Google Scholar
6. Karlin, S. and Studden, W. J., Tchebycheff systems: with applications in analysis and statistics (Wiley, New York, 1966).Google Scholar
7. Krein, M. G., The ideas of P. L. Chebysev and A. A. Markov in the theory of limiting values of integrals and their future development, Uspehi Mat. Nauk (N. S.) 6 (1951), no. 4 (44), 3–120; Am. Math. Soc. Transi, Ser. 2, 12, 1–122.Google Scholar
8. Lorentz, G. G., Approximation of functions (Holt, Rinehart and Winston, N.Y., 1966).Google Scholar
9. Rice, J. R., The approximation of functions, Vol. II (Addison-Wesley, Bath, 1969).Google Scholar
10. Shohat, J. A. and Tamarkin, J. D., The problem of moments, Am. Math. Soc. Surveys nos. 7 (1943).CrossRefGoogle Scholar