Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Burckel, R.B
and
Saeki, Sadahiro
1984.
Closure and homomorphic properties in B∗-algebras via functions which operate.
Journal of Mathematical Analysis and Applications,
Vol. 98,
Issue. 1,
p.
211.
2008.
Das Operationsteam.
p.
17.

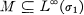 be a 1 inear map of ikf into
be a 1 inear map of ikf into 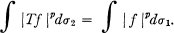
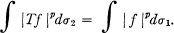 is a linear isometry in the L
is a linear isometry in the L