For 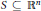$S\,\subseteq \,{{\mathbb{R}}^{n}}$ a set 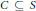$C\,\subseteq \,S$ is an $m$-clique if the convex hull of no $m$-element subset of $C$ is contained in $S$. We show that there is essentially just one way to construct a closed set 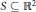$S\,\subseteq \,{{\mathbb{R}}^{2}}$ without an uncountable 3-clique that is not the union of countably many convex sets. In particular, all such sets have the same convexity number; that is, they require the same number of convex subsets to cover them. The main result follows from an analysis of the convex structure of closed sets in 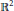${{\mathbb{R}}^{2}}$ without uncountable 3-cliques in terms of clopen, 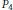${{P}_{4}}$-free graphs on Polish spaces.