Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-20T01:40:25.767Z Has data issue: false hasContentIssue false
  • English
  • Français

Amenable and inner amenable actions and approximation properties for crossed products by locally compact groups

Published online by Cambridge University Press:  24 May 2021

Andrew McKee  and
Reyhaneh Pourshahami
Andrew McKee*
Affiliation:
Faculty of Mathematics, University of Białystok, ul. K. Ciołkowskiego 1M, Białystok15-425, Poland
Reyhaneh Pourshahami
Affiliation:
Department of Mathematics, Kharazmi University, 50 Taleghani Avenue, 15618Tehran, Iran e-mail: std_reyhaneh.pourshahami@khu.ac.ir
*
e-mail: amckee240@qub.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Amenable actions of locally compact groups on von Neumann algebras are investigated by exploiting the natural module structure of the crossed product over the Fourier algebra of the acting group. The resulting characterization of injectivity for crossed products generalizes a result of Anantharaman-Delaroche on discrete groups. Amenable actions of locally compact groups on 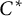$C^*$ -algebras are investigated in the same way, and amenability of the action is related to nuclearity of the corresponding crossed product. A survey is given to show that this notion of amenable action for 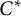$C^*$ -algebras satisfies a number of expected properties. A notion of inner amenability for actions of locally compact groups is introduced, and a number of applications are given in the form of averaging arguments, relating approximation properties of crossed product von Neumann algebras to properties of the components of the underlying 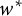$w^*$ -dynamical system. We use these results to answer a recent question of Buss, Echterhoff, and Willett.

Keywords

Amenable actioninner amenable actioncrossed productoperator moduleinjectivity
Type
Article
Information
Canadian Mathematical Bulletin , Volume 65 , Issue 2 , June 2022 , pp. 381 - 399
Check for updates
Copyright
© Canadian Mathematical Society 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anantharaman-Delaroche, C., Action moyennable d’un groupe localement compact sur une algèbre de von Neumann. Math. Scand. 45(1979), no. 2, 289–304.CrossRefGoogle Scholar
Anantharaman-Delaroche, C., Action moyennable d’un groupe localement compact sur une algèbre de von Neumann. II. Math. Scand. 50(1982), no. 2, 251–268.CrossRefGoogle Scholar
Anantharaman-Delaroche, C., Systèmes dynamiques non commutatifs et moyennabilité. Math. Ann. 279(1987), no. 2, 297–315.CrossRefGoogle Scholar
Anantharaman-Delaroche, C., Amenable correspondences and approximation properties for von Neumann algebras. Pacific J. Math. 171(1995), no. 2, 309–341.CrossRefGoogle Scholar
Anantharaman-Delaroche, C., Amenability and exactness for dynamical systems and their ${C}^{\ast }$ -algebras . Trans. Amer. Math. Soc. 354(2002), no. 10, 4153–4178.CrossRefGoogle Scholar
Bearden, A. and Crann, J., Amenable dynamical systems over locally compact groups. Ergodic Theory Dynam. Systems. To appear. arXiv:2004.01271 Google Scholar
Bearden, A. and Crann, J., A weak expectation property for operator modules, injectivity and amenable actions. Internat. J. Math. 32(2021), no. 2, 2150005. arXiv:2009.05690 CrossRefGoogle Scholar
Brodzki, J., Cave, C., and Li, K., Exactness of locally compact groups. Adv. Math. 312(2017), 209–233.CrossRefGoogle Scholar
Brown, N. P. and Ozawa, N., C*-algebras and finite-dimensional approximations . Graduate Studies in Mathematics, 88, American Mathematical Society, Providence, RI, 2008.CrossRefGoogle Scholar
Buss, A., Echterhoff, S., and Willett, R., Injectivity, crossed products, and amenable group actions . In: K-theory in algebra, analysis and topology, Editors: Cortiñas, Guillermo and Weibel, Charles A., American Mathematical Society, Providence, RI, 2020, pp. 105–137.Google Scholar
Buss, A., Echterhoff, S., and Willett, R., Amenability and weak containment for actions of locally compact groups on ${C}^{\ast }$ -algebras. Preprint, 2021. arXiv:2003.03469 Google Scholar
Connes, A., Classification of injective factors. $\textit{Cases}\; II_{1}$ , $II_{\infty }$ , $III_{\lambda }$ , $\lambda \neq 1$ . Ann. of Math. (2) 104(1976), no. 1, 73–115.CrossRefGoogle Scholar
Crann, J., Amenability and covariant injectivity of locally compact quantum groups II. Canad. J. Math. 69(2017), no. 5, 1064–1086.CrossRefGoogle Scholar
Crann, J., Inner amenability and approximation properties of locally compact quantum groups. Indiana Univ. Math. J. 68(2019), no. 6, 1721–1766.CrossRefGoogle Scholar
Crann, J., Finite presentation, the local lifting property, and local approximation properties of operator modules. J. Funct. Anal. To appear. arXiv:2008.09102 Google Scholar
Crann, J. and Neufang, M., Amenability and covariant injectivity of locally compact quantum groups. Trans. Amer. Math. Soc. 368(2016), no. 1, 495–513.CrossRefGoogle Scholar
Crann, J. and Tanko, Z., On the operator homology of the Fourier algebra and its $cb$ -multiplier completion . J. Funct. Anal. 273(2017), no. 7, 2521–2545.CrossRefGoogle Scholar
Effros, E. G., Property $\varGamma$ and inner amenability . Proc. Amer. Math. Soc. 47(1975), 483–486.Google Scholar
Effros, E. G. and Ruan, Z.-J., Operator spaces . London Mathematical Society Monographs, New Series, 23, The Clarendon Press and Oxford University Press, New York, 2000.Google Scholar
Eymard, P., L’algèbre de Fourier d’un groupe localement compact. Bull. Soc. Math. France 92(1964), 181–236.CrossRefGoogle Scholar
Haagerup, U., Group ${C}^{\ast }$ -algebras without the completely bounded approximation property . J. Lie Theory 26(2016), no. 3, 861–887.Google Scholar
Ikunishi, A., The ${W}^{\ast }$ -dynamical system associated with a ${C}^{\ast }$ -dynamical system, and unbounded derivations . J. Funct. Anal. 79(1988), no. 1, 1–8.CrossRefGoogle Scholar
Kirchberg, E. and Wassermann, S., Permanence properties of ${C}^{\ast }$ -exact groups . Doc. Math. 4(1999), 513–558.Google Scholar
Lance, C., On nuclear ${C}^{\ast }$ -algebras . J. Funct. Anal. 12(1973), 157–176.CrossRefGoogle Scholar
Lau, A. T. M. and Paterson, A. L. T., Inner amenable locally compact groups. Trans. Amer. Math. Soc. 325(1991), no. 1, 155–169.CrossRefGoogle Scholar
McKee, A., Multipliers and duality for group actions. Preprint, 2019. arXiv:1912.10700 Google Scholar
McKee, A., Skalski, A., Todorov, I. G., and Turowska, L., Positive Herz–Schur multipliers and approximation properties of crossed products. Math. Proc. Cambridge Philos. Soc. 165(2018), no. 3, 511–532.CrossRefGoogle Scholar
Nakagami, Y. and Takesaki, M., Duality for crossed products of von Neumann algebras . Lecture Notes in Mathematics, 731, Springer, Berlin and Germany, 1979.CrossRefGoogle Scholar
Ozawa, N. and Suzuki, Y., On characterizations of amenable ${C}^{\ast }$ -dynamical systems and new examples. Preprint, 2020. arXiv:2011.03420 CrossRefGoogle Scholar
Paterson, A. L. T., Amenability . Mathematical Surveys and Monographs, 29, American Mathematical Society, Providence, RI, 1988.CrossRefGoogle Scholar
Renaud, P. F., Invariant means on a class of von Neumann algebras. Trans. Amer. Math. Soc. 170(1972), 285–291.CrossRefGoogle Scholar
Suzuki, Y., Simple equivariant ${C}^{\ast }$ -algebras whose full and reduced crossed products coincide . J. Noncommut. Geom. 13(2019), no. 4, 1577–1585.CrossRefGoogle Scholar
Takesaki, M., Theory of operator algebras. III . Encyclopaedia of Mathematical Sciences, 127, Springer, Berlin and Germany, 2003. Operator Algebras and Non-Commutative Geometry, 8.CrossRefGoogle Scholar
Williams, D. P., Crossed products of C*-algebras . Mathematical Surveys and Monographs, 134, American Mathematical Society, Providence, RI, 2007.CrossRefGoogle Scholar
Zimmer, R. J., Hyperfinite factors and amenable ergodic actions. Invent. Math. 41(1977), no. 1, 23–31.CrossRefGoogle Scholar
Zimmer, R. J., On the von Neumann algebra of an ergodic group action. Proc. Amer. Math. Soc. 66(1977), no. 2, 289–293.CrossRefGoogle Scholar
Zimmer, R. J., Amenable ergodic group actions and an application to Poisson boundaries of random walks. J. Funct. Anal. 27(1978), no. 3, 350–372.CrossRefGoogle Scholar