Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-23T18:53:12.419Z Has data issue: false hasContentIssue false
  • English
  • Français

An elliptic curve analogue of Pillai’s lower bound on primitive roots

Part of: Arithmetic algebraic geometry Curves

Published online by Cambridge University Press:  29 June 2021

Steven Jin  and
Lawrence C. Washington
Steven Jin*
Affiliation:
Department of Mathematics, University of Maryland, College Park, MD 20742, USA e-mail: lcw@umd.edu
Lawrence C. Washington
Affiliation:
Department of Mathematics, University of Maryland, College Park, MD 20742, USA e-mail: lcw@umd.edu
*
e-mail: sjin6816@umd.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 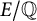$E/\mathbb {Q}$ be an elliptic curve. For a prime p of good reduction, let 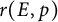$r(E,p)$ be the smallest non-negative integer that gives the x-coordinate of a point of maximal order in the group 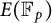$E(\mathbb {F}_p)$ . We prove unconditionally that 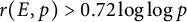$r(E,p)> 0.72\log \log p$ for infinitely many p, and 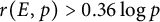$r(E,p)> 0.36 \log p$ under the assumption of the Generalized Riemann Hypothesis. These can be viewed as elliptic curve analogues of classical lower bounds on the least primitive root of a prime.

Keywords

Elliptic curvesfinite fieldsprimitive root

MSC classification

Primary: 11G20: Curves over finite and local fields 14H52: Elliptic curves
Type
Article
Information
Canadian Mathematical Bulletin , Volume 65 , Issue 2 , June 2022 , pp. 496 - 505
Check for updates
Copyright
© Canadian Mathematical Society 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahn, J.-H. and Kwon, S.-H., An explicit upper bound for the least prime ideal in the Chebotarev density theorem. Ann. l’Inst. Fourier 69(2019), no. 3, 1411–1458.CrossRefGoogle Scholar
Burgess, D. A., On character sums and primitive roots. Proc. Lond. Math. Soc. (3) 12(1962), 179–192.CrossRefGoogle Scholar
Dubrois, J. and Dumas, J.-G., Efficient polynomial time algorithms computing industrial-strength primitive roots. Inform. Process. Lett. 97(2006), no. 2, 41–45.CrossRefGoogle Scholar
Erdős, P., Least primitive root of a prime. Bull. Amer. Math. Soc. 55(1945), 131–132.CrossRefGoogle Scholar
Erdős, P. and Shapiro, H. N., On the least primitive root of a prime. Pacific J. Math. 7(1957), no. 1, 861–865.CrossRefGoogle Scholar
Fridlender, V. R., On the least n-th power non-residue. Proc. USSR Acad. Sci. 66(1949), 351–352.Google Scholar
Graham, S. W. and Ringrose, C. J.. Lower bounds for least quadratic non-residues . In: Analytic number theory (Allerton Park, IL, 1989), Progr. Math., 85, Birkhauser, Boston, MA, 1990, pp. 269–309.CrossRefGoogle Scholar
Hua, L. K., On the least primitive root of a prime. Bull. Amer. Math. Soc. 48(1942), 726–730.CrossRefGoogle Scholar
Kadiri, H. and Wong, P., Primes in the Chebotarev density theorem for all number fields (with an appendix by Andrew Fiori). Preprint, 2021. arxiv.org/pdf/2105.14181.pdf CrossRefGoogle Scholar
Kohel, D. R. and Shparlinski, I. E., On exponential sums and group generators for elliptic curves over finite fields . In: Algorithmic number theory, Lecture Notes in Computer Science, 1838, Springer, Berlin, Heidelberg, 2000.Google Scholar
Lagarias, J. C. and Odlyzko, A. M., Effective versions of the Chebotarev density theorem . In: Algebraic number fields: L-functions and Galois properties (Proc. Sympos., Univ. Durham, Durham, 1975), Academic Press, London, 1977, pp. 409–464.Google Scholar
Lang, S., Algebraic number theory. Graduate Texts in Math, 110, Springer-Verlag, New York, 1986.CrossRefGoogle Scholar
Montgomery, H. L., Topics in multiplicative number theory. Lecture Notes in Math, 227, Springer-Verlag, New York, 1971.CrossRefGoogle Scholar
Pillai, S., On the smallest primitive root of a prime. J. Indian Math. Soc. 8(1944), 14–17.Google Scholar
Salié, H., Über den kleinsten positiven quadratischen Nichtrest nach einer Primzahl. Math. Nachr. 3(1949), 7–8.CrossRefGoogle Scholar
Shoup, V., Searching for primitive roots in prime fields. Math. Comp. 58(1992), 369–380.CrossRefGoogle Scholar
Stein, W. A. et al., Sage Mathematics Software (Online version: April 2021). The Sage Development Team. https://sagecell.sagemath.orgGoogle Scholar
Toyama, H., A note on the different of the composed field. Kodai Math. Sem. Rep. 7(1955), no. 2, 43–44.CrossRefGoogle Scholar
Vinogradov, I. M., On the least primitive root of a prime. Dokl. Akad. Nauk, S.S.S.R 1 (1930), 7–11.Google Scholar