Hostname: page-component-6bf8c574d5-n2sc8 Total loading time: 0 Render date: 2025-03-06T16:36:56.575Z Has data issue: false hasContentIssue false
  • English
  • Français

Perfectly packing a cube by cubes of nearly harmonic sidelength

Part of: Discrete geometry

Published online by Cambridge University Press:  14 February 2023

Rory McClenagan
Rory McClenagan*
Affiliation:
Department of Mathematics and Statistics, University of Northern British Columbia, Prince George, BC V2N4Z9, Canada
*
e-mail: mcclenaga@unbc.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

Let d be an integer greater than 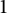$1$, and let t be fixed such that 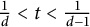$\frac {1}{d} < t < \frac {1}{d-1}$. We prove that for any 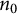$n_0$ chosen sufficiently large depending on t, the d-dimensional cubes of sidelength 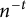$n^{-t}$ for 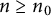$n \geq n_0$ can perfectly pack a cube of volume 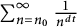$\sum _{n=n_0}^{\infty } \frac {1}{n^{dt}}$. Our work improves upon a previously known result in the three-dimensional case for when 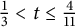$\frac {1}{3} < t \leq \frac {4}{11} $ and 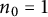$n_0 = 1$ and builds upon recent work of Terence Tao in the two-dimensional case.

Keywords

Packingsquare packingcube packingMeirMoser

MSC classification

Primary: 52C17: Packing and covering in $n$ dimensions
Type
Article
Information
Canadian Mathematical Bulletin , Volume 66 , Issue 3 , September 2023 , pp. 1061 - 1071
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research of the author is partially supported by NSERC CGS-M.

References

Grzegorek, P. and Januszewski, J., A note on three Moser’s problems and two Paulhus’ lemmas . J. Combin. Theory Ser. A 162(2019), 222–230.CrossRefGoogle Scholar
Januszewski, J. and Zielonka, L., A note on perfect packing of d-dimensional cubes . Sib. Electron. Math. Rep. 17(2007), 1009–1012.Google Scholar
Januszewski, J. and Zielonka, L., A note on perfect packing of squares and cubes . Acta Math. Hungar. 163(2021), 530–537.CrossRefGoogle Scholar
Joós, A., On packing of rectangles in a rectangle . Discret. Math. 341(2018), 2544–2552.CrossRefGoogle Scholar
Joós, A., Perfect packing of cubes . Acta Math. Hungar. 156(2018), 375–384.CrossRefGoogle Scholar
Joós, A., Perfect packing of $d$ -cubes . Sib. Electron. Math. Rep. 17(2020), 853–864.Google Scholar
Martin, G., Compactness theorems for geometric packings . J. Combin. Theory Ser. A 97(2002), 225–238.CrossRefGoogle Scholar
Meir, A. and Moser, L., On packing of squares and cubes . J. Combin. Theory Ser. A 5(1968), 126–134.CrossRefGoogle Scholar
Paulhus, M. M., An algorithm for packing squares . J. Combin. Theory Ser. A 82(1998), 147–157.CrossRefGoogle Scholar
Tao, T., Perfectly packing a square by squares of nearly harmonic sidelength. Preprint, 2022. arXiv:2202.03594 CrossRefGoogle Scholar