No CrossRef data available.
Article contents
Some results on the Flynn–Poonen–Schaefer conjecture
Part of:
Complex dynamical systems
Arithmetic and non-Archimedean dynamical systems
Algebraic number theory: local and $p$-adic fields
General field theory
Published online by Cambridge University Press: 11 August 2021
Abstract
For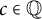 
$c \in \mathbb {Q}$
, consider the quadratic polynomial map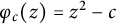 
$\varphi _c(z)=z^2-c$
. Flynn, Poonen, and Schaefer conjectured in 1997 that no rational cycle of 
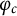$\varphi _c$
under iteration has length more than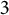 
$3$
. Here, we discuss this conjecture using arithmetic and combinatorial means, leading to three main results. First, we show that if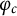 
$\varphi _c$
admits a rational cycle of length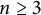 
$n \ge 3$
, then the denominator of c must be divisible by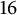 
$16$
. We then provide an upper bound on the number of periodic rational points of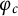 
$\varphi _c$
in terms of the number s of distinct prime factors of the denominator of c. Finally, we show that the Flynn–Poonen–Schaefer conjecture holds for 
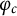$\varphi _c$
if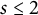 
$s \le 2$
, i.e., if the denominator of c has at most two distinct prime factors.
MSC classification
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2021
References
Adam, A. and Fares, Y.,
On two affine-like dynamical systems in a local field
. J. Number Theory. 132(2012), 2892–2906.CrossRefGoogle Scholar
Benedetto, R.,
Preperiodic points of polynomials over global fields
. J. Reine Angew. Math. 608(2007), 123–153.Google Scholar
Call, G. and Goldstine, S.,
Canonical heights on projective space
. J. Number Theory. 63(1997), 211–243.CrossRefGoogle Scholar
Eliahou, S. and Fares, Y.,
Poonen’s conjecture and Ramsey numbers
. Discrete Appl. Math. 209(2016), 102–106.10.1016/j.dam.2015.07.038CrossRefGoogle Scholar
Fares, Y., On the iteration over ℝ of rational quadratic polynomials. Preprint, 2020. https://hal.archives-ouvertes.fr/hal-02534351/document
Google Scholar
Flynn, E. V., Poonen, B., and Schaefer, E. F.,
Cycles of quadratic polynomials and rational points on a genus-2 curve
. Duke Math. J. 90(1997), 435–463.10.1215/S0012-7094-97-09011-6CrossRefGoogle Scholar
Morton, P.,
Arithmetic properties of periodic points of quadratic maps
. Acta Arith. 62(1992), 343–372.10.4064/aa-62-4-343-372CrossRefGoogle Scholar
Narkiewicz, W.,
Cycle-lengths of a class of monic binomials
. Funct. Approx. Comment. Math. 42(2010), 2, 163–168.10.7169/facm/1277811639CrossRefGoogle Scholar
Narkiewicz, W.,
On a class of monic binomials
. Proc. Steklov Inst. Math. 280(2013), suppl. 2, S65–S70.10.1134/S0081543813030073CrossRefGoogle Scholar
Northcott, D.,
Periodic points on an algebraic variety
. Ann. of Math. (2). 51(1950), 167–177.10.2307/1969504CrossRefGoogle Scholar
Pezda, T.,
Polynomial cycles in certain local domains
. Acta Arith. 66(1994), 11–22.10.4064/aa-66-1-11-22CrossRefGoogle Scholar
Poonen, B., The classification of rational preperiodic points of quadratic polynomials over ℚ: a refined conjecture. Math. Z. 228(1998), 11–29.10.1007/PL00004405CrossRefGoogle Scholar
Silverman, J. H., The arithmetic of dynamical systems, Graduate Texts in Mathematics, 241, Springer, New York, 2007.CrossRefGoogle Scholar
Stoll, M.,
Rational 6-cycles under iteration of quadratic polynomials
. LMS J. Comput. Math. 11(2008), 367–380.10.1112/S1461157000000644CrossRefGoogle Scholar
Walde, R. and Russo, P., Rational periodic points of the quadratic function Qc = x 2 + c. Amer. Math. Monthly. 101(1994), 318–331.Google Scholar
Zieve, M., Cycles of polynomial mappings. Ph.D. thesis, UC Berkeley, 1996.Google Scholar