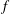Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
AAAVoloch, José Felipe
2020.
Commitment schemes and diophantine equations.
Open Book Series,
Vol. 4,
Issue. 1,
p.
1.
Shparlinski, Igor E.
and
Felipe Voloch, José
2022.
Corrections to “Value sets of sparse polynomials”.
Canadian Mathematical Bulletin,
Vol. 65,
Issue. 4,
p.
1071.