Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-22T07:15:27.807Z Has data issue: false hasContentIssue false
  • English
  • Français

Alexandroff Manifolds and Homogeneous Continua

Published online by Cambridge University Press:  20 November 2018

A. Karassev ,
V. Todorov  and
V. Valov
A. Karassev
Affiliation:
Department of Computer Science and Mathematics, Nipissing University, North Bay, ON, P1B 8L7 e-mail: alexandk@nipissingu.caveskov@nipissingu.ca
V. Todorov
Affiliation:
Department of Mathematics, UACG, Sofia, Bulgaria e-mail: vtt-fte@uacg.bg
V. Valov
Affiliation:
Department of Computer Science and Mathematics, Nipissing University, North Bay, ON, P1B 8L7 e-mail: alexandk@nipissingu.caveskov@nipissingu.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove the following result announced by the second and third authors: Any homogeneous, metric 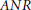$ANR$-continuum is a 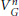$V_{G}^{n}$-continuum provided 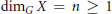${{\dim}_{G}}X\,=\,n\,\ge \,1$ and 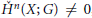${{\overset{\vee }{\mathop{H}}\,}^{n}}\left( X;\,G \right)\,\ne \,0$, where $G$ is a principal ideal domain. This implies that any homogeneous $n$-dimensional metric 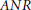$ANR$-continuum is a 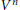${{V}^{n}}$-continuum in the sense of Alexandroff. We also prove that any finite-dimensional cyclic in dimension $n$ homogeneous metric continuum 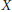$X$, satisfying 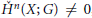${{\overset{\vee }{\mathop{H}}\,}^{n}}\left( X;\,G \right)\,\ne \,0$ for some group $G$ and 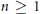$n\,\ge \,1$, cannot be separated by a compactum 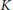$K$ with 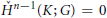${{\overset{\vee }{\mathop{H}}\,}^{n-1}}\left( K;\,G \right)\,=\,0$ and ${{\dim}_{G}}K\,\le \,n\,-\,1$. This provides a partial answer to a question of Kallipoliti–Papasoglu as to whether a two-dimensional homogeneous Peano continuum can be separated by arcs.

Keywords

54F4554F15Cantor manifoldcohomological dimensioncohomology groupshomogeneous compactumseparatorVn-continuum
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 57 , Issue 2 , 14 June 2014 , pp. 335 - 343
Copyright
Copyright © Canadian Mathematical Society 2014

Footnotes

The first author was partially supported by NSERC Grant 257231-09. The third author was partially supported by NSERC Grant 261914-08.

References

[1] Alexandroff, P. S., Die Kontinua (V p )–eine Verschärfung der Cantorschen Mannigfaltigkeiten. Monatsh. Math. 61 (1957), 67–76.http://dx.doi.org/10.1007/BF01306919 CrossRefGoogle Scholar
[2] Bing, R. H. and K. Borsuk, Some remarks concerning topologically homogeneous spaces. Ann. of Math. 81 (1965), 100–111.http://dx.doi.org/10.2307/1970385 CrossRefGoogle Scholar
[3] Choi, J. S., Properties of n-bubbles in n-dimensional compacta and the existence of (n–1)-bubbles in n-dimensional clcn compacta. Topology Proc. 23 (1998), Spring, 101–120.Google Scholar
[4] Dranishnikov, A. N., On a problem of Aleksandrov P. S.. Mat. Sb. 135 (1988), no. 4, 551–557, 560; translation in Math. USSR-Sb. 63 (1989), no. 2, 539–545.Google Scholar
[5] Dranishnikov, A. N., Universal Menger compacta and universal mappings. (Russian) Mat. Sb. 129 (1986), no. 1, 121–139, 160.Google Scholar
[6] Dydak, J. and Koyama, A., Cohomological dimension of locally connected compacta. Topology Appl. 113 (2001), no. 1–3, 39–50.http://dx.doi.org/10.1016/S0166-8641(00)00018-3 CrossRefGoogle Scholar
[7] Dydak, J. and Wash, J., Infinite-dimensional compacta having cohomological dimension two: an application of the Sullivan conjecture. Topology 32 (1993), no. 1, 93–104.http://dx.doi.org/10.1016/0040-9383(93)90040-3 CrossRefGoogle Scholar
[8] Effros, E. G., Transformation groups and C*-algebras. Ann. of Math. 81 (1965), 38–55.http://dx.doi.org/10.2307/1970381 Google Scholar
[9] Hadžiivanov, N., Strong Cantor manifolds. (Russian) C. R. Acad. Bulgare Sci. 30 (1977), no. 9. 1247–1249.Google Scholar
[10] Hadžiivanov, N. and Todorov, V., On non-Euclidean manifolds. (Russian) C. R. Acad. Bulgare Sci. 33 (1980), no. 4, 449–452.Google Scholar
[11] Kallipoliti, M. and Papasoglu, P., Simply connected homogeneous continua are not separated by arcs. Topology Appl. 154 (2007), no. 17, 3039–3047.http://dx.doi.org/10.1016/j.topol.2007.06.016 Google Scholar
[12] Karassev, A., Krupski, P., Todorov, V., and Valov, V., Generalized Cantor manifolds and homogeneity. Houston J. Math. 38 (2012), no. 2, 583–609.Google Scholar
[13] Karimov, U. and Repovš, D., On Hn-bubles in n-dimensional compacta. Colloq. Math. 75 (1998), no. 1, 39–51.10.4064/cm-75-1-39-51CrossRefGoogle Scholar
[14] Krupski, P., Homogeneity and Cantor manifolds. Proc. Amer. Math. Soc. 109 (1990), no. 4, 1135–1142.http://dx.doi.org/10.1090/S0002-9939-1990-1009992-7 CrossRefGoogle Scholar
[15] Kuperberg, W., On certain homological properties of finite-dimensional compacta. Carries, minimal carries and bubbles. Fund. Math. 83 (1973), no. 1, 7–23.Google Scholar
[16] Stefanov, S. T., A cohomological analogue of Vn-continua and a theorem of Mazurkiewicz. (Russian) Serdica 12 (1986), no. 1, 88–94.Google Scholar
[17] Todorov, V., Irreducibly cyclic compacta and Cantor manifolds. Proc. of the Tenth Spring Conf. of the Union of Bulg. Math. (Sunny Beach, April 6-9, 1981).Google Scholar
[18] Todorov, V. and Valov, V., Generalized Cantor manifolds and indecomposable continua. Questions Answers Gen. Topology 30 (2012), no. 2, 93–102.Google Scholar
[19] Urysohn, P., Memoire sur les multiplicites cantoriennes. Fund. Math. 7 (1925), 30–137.10.4064/fm-7-1-30-137CrossRefGoogle Scholar
[20] Yokoi, K., Bubbly continua and homogeneity. Houston J. Math. 29 (2003), no. 2, 337–343.Google Scholar