Hostname: page-component-cb9f654ff-p5m67 Total loading time: 0 Render date: 2025-09-02T11:12:55.723Z Has data issue: false hasContentIssue false
  • English
  • Français

An estimate for the composition of rough singular integral operators

Part of: Special classes of linear operators Harmonic analysis in several variables

Published online by Cambridge University Press:  07 December 2020

Xiangxing Tao  and
Guoen Hu
Xiangxing Tao
Affiliation:
Department of Mathematics, School of Science, Zhejiang University of Science and Technology, Hangzhou 310023, P.R. China e-mail: xxtao@zust.edu.cn
Guoen Hu*
Affiliation:
School of Applied Mathematics, Beijing Normal University, Zhuhai 519087, P.R. China
*
e-mail: guoenxx@163.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Let $\Omega $ be homogeneous of degree zero and have mean value zero on the unit sphere 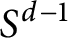${S}^{d-1}$, 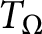$T_{\Omega }$ be the convolution singular integral operator with kernel 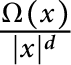$\frac {\Omega (x)}{|x|^d}$. In this paper, we prove that if 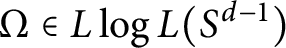$\Omega \in L\log L(S^{d-1})$, and U is an operator which is bounded on 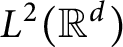$L^2(\mathbb {R}^d)$ and satisfies the weak type endpoint estimate of 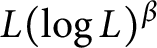$L(\log L)^{\beta }$ type, then the composition operator 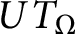$UT_{\Omega }$ satisfies a weak type endpoint estimate of 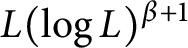$L(\log L)^{\beta +1}$ type.

Keywords

Rough singular integral operatorcomposite operatorweak type endpoint estimate

MSC classification

Primary: 42B20: Singular and oscillatory integrals (Calderón-Zygmund, etc.)
Secondary: 47B33: Composition operators

Information

Type
Article
Information
Canadian Mathematical Bulletin , Volume 64 , Issue 4 , December 2021 , pp. 911 - 922
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The research of X.T was supported by the NNSF of China under grant #11771399, and the research of G.H. (corresponding author) was supported by the NNSF of China under grant #11871108.

References

Benea, C. and Bernicot, F., Conservation de certaines propriétés á travers un contrôle épars d’un opérateur et applications au projecteur de Leray–Hopf. Preprint, 2020. arxiv:1703:00228 Google Scholar
Calderón, A. P., Algebras of singular integral operators . In: Singular integrals (Chicago, IL, 1966), Proc. Sympos. Pure Math., Amer. Math. Soc., Providence, RI, 1967, pp. 18–55.CrossRefGoogle Scholar
Calderón, A. P., Algebras of singular integral operators . Proc. Int. Congr. Math. (Moscow, Russia, 1966), Mir, Moscow, Russia, 1968, pp. 393–395.Google Scholar
Calderón, A. P. and Zygmund, A., On the existence of certain singular integrals . Acta Math. 88(1952), 85–139.CrossRefGoogle Scholar
Calderón, A. P. and Zygmund, A., On singular integrals . Amer. J. Math. 78(1956), 289–309.CrossRefGoogle Scholar
Calderón, A. P. and Zygmund, A., Algebras of certain singular operators . Amer. J. Math. 78(1956), 310–320.CrossRefGoogle Scholar
Carozza, N. and Passarelli di Napoli, A., Composition of maximal operators . Publ. Mat. 40(1996), 397–409.CrossRefGoogle Scholar
Christ, M., Inversion in some algebras of singular integral operators . Rev. Mat. Iberoam. 4(1988), 219–225.CrossRefGoogle Scholar
Christ, M. and Rubio de Francia, J. -L., Weak type (1, 1) bounds for rough operators, II . Invent. Math. 93(1988), 225–237.CrossRefGoogle Scholar
Duoandikoetxea, J. and Rubio de Francia, J. L., Maximal and singular integrals via Fourier transform estimates . Invent. Math. 84(1986), 541–561.CrossRefGoogle Scholar
Grafakos, L., Modern Fourier analysis . 3rd ed., Graduate Texts in Mathematics, 250, Springer, New York, 2014.Google Scholar
Hu, G., Weighted weak type endpoint estimates for the composition of Calderón–Zygmund operators . J. Aust. Math. Soc. 109(2020), 320–339.CrossRefGoogle Scholar
Hu, G., Lai, X., and Xue, Q., On the composition of rough singular integral operators . J. Geom. Anal (2020). https://doi.org/10.1007/s12220-020-00374-6 Google Scholar
Lerner, A. K., A weak type estimates for rough singular integrals . Rev. Mat. Iberoam. 35(2019), 1583–1602.CrossRefGoogle Scholar
Muckenhoupt, B. and Wheeden, R. L., Weighted norm inequalities for singular and fractional integrals . Trans. Amer. Math. Soc. 161(1971), 249–258.CrossRefGoogle Scholar
Nagel, A., Ricci, F., Stein, E. M., and Wainger, S., Algebras of singular integral operators with kernels controlled by multiple norms. Memoirs Amer. Math. Soc., 256, no. 1230, Amer. Math. Soc., Providence, RI, 2018.Google Scholar
Phone, D. H. and Stein, E. M., Some further classes of pseudo-differential and singular integral operators arising in boundary-value problems I, composition of operators . Amer. J. Math. 104(1982), 141–172.CrossRefGoogle Scholar
Ricci, F. and Weiss, G., A characterization of H1 (S n−1). In: Wainger, S. and Weiss, G. (eds.), Proc. Sympos. Pure Math., 35 I, Amer. Math. Soc., Providence, RI, 1979, pp. 289–294.Google Scholar
Seeger, A., Singular integral operators with rough convolution kernels . J. Amer. Math. Soc. 9(1996), 95–105.CrossRefGoogle Scholar
Strichartz, R. S., Compositions of singular integral operators . J. Funct. Anal. 49(1982), 91–127.CrossRefGoogle Scholar