Let 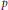$p$ be a prime, and let 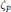${{\zeta }_{p}}$ be a primitive 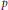$p$-th root of unity. The lattices in Craig's family are 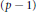$(p\,-\,1)$-dimensional and are geometrical representations of the integral 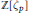$\mathbb{Z}[{{\zeta }_{p}}]$-ideals 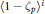${{\left\langle 1\,-\,{{\zeta }_{p}} \right\rangle }^{i}}$, where $i$ is a positive integer. This lattice construction technique is a powerful one. Indeed, in dimensions 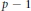$p\,-\,1$ where 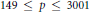$149\,\le \,p\,\le \,3001$, Craig's lattices are the densest packings known. 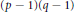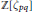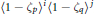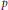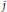Motivated by this, we construct $(p\,-\,1)(q\,-\,1)$-dimensional lattices from the integral $\mathbb{Z}[{{\zeta }_{pq}}]$-ideals ${{\left\langle 1\,-\,{{\zeta }_{p}} \right\rangle }^{i}}{{\left\langle 1\,-\,{{\zeta }_{q}} \right\rangle }^{j}}$, where $p$ and $q$ are distinct primes and $i$ and $j$ are positive integers. In terms of sphere-packing density, the new lattices and those in Craig's family have the same asymptotic behavior. In conclusion, Craig's family is greatly extended while preserving its sphere-packing properties.