Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-21T22:10:47.633Z Has data issue: false hasContentIssue false
  • English
  • Français

A Characterization of C*-normed Algebras via Positive Functionals

Published online by Cambridge University Press:  20 November 2018

Marina Haralampidou ,
Mohamed Oudadess ,
Lourdes Palacios  and
Carlos Signoret
Marina Haralampidou
Affiliation:
Department of Mathematics, University of Athens, Panepistimioupolis, Athens 1584, Greece, e-mail: mharalam@math.uoa.gr
Mohamed Oudadess
Affiliation:
Ecole Normale Supérieure, B.P 5118, Takaddoum, 10105 Rabat, Morocco, e-mail: oudadesshha@gmail.com
Lourdes Palacios
Affiliation:
Universidad Autónoma Metropolitana Iztapalapa, Mexico City 09340, Mexico, e-mail: pafa@xanum.uam.mx
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We give a characterization of 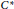${{C}^{*}}$-normed algebras, among certain involutive normed ones. This is done through the existence of enough specific positive functionals. The same question is also examined in some non normed (topological) algebras.

Keywords

46H0546K05C*-normed algebraC*-algebra(pre-)locally C*-algebrapre-C*-bornological algebrapositive functionallocally uniformly A-convex algebraperfect locally m-convex algebraC*-subnormable algebra*-subnormable algebra
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 61 , Issue 1 , 01 March 2018 , pp. 114 - 123
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Allan, G. R., Dales, H. G., and McClure, J. P., Pseudo-Banach algebras. Studia Math. 40 (1971), 55–69.Google Scholar
[2] Apostol, C., b*-algebras and their representations. J. London Math. Soc. 3 (1971), 30–38. http://dx.doi.Org/10.1112/jlms/s2-3.1.30.Google Scholar
[3] Bourbaki, N., Theorie des Ensembles. Chap. 3, Hermann, Paris, 1967.Google Scholar
[4] Cochran, A. C., Representation of A-convex algebras. Proc. Amer. Math. Soc. 41 (1973), 473–479. http://dx.doi.Org/10.2307/203911 6.Google Scholar
[5] Cochran, A. C., Keown, R., and Williams, C. R., On a class of topological algebras. Pacific J. Math. 34 (1970), 17–25. http://dx.doi.org/10.2140/pjm.1970.34.17.Google Scholar
[6] Doran, R. S., Research problems: Does there exist a Banach *-algebra without identity with no nonzero positive functionals? Amer. Math. Monthly 87 (1980), 474–475. http://dx.doi.Org/10.2307/2320257.Google Scholar
[7] Fragoulopoulou, M., Topological algebras with Involution. North Holland Mathematics Studies, 200. Elsevier Science, Amsterdam, 2005.Google Scholar
[8] Gorbachev, N. V., An example of a Banach âlgebra without identity and with no nonzero positive functionals. Uspekhi Mat. Nauk 38(1983), 189.Google Scholar
[9] Haralampidou, M., The Krull nature oflocally C*-algebras. Function Spaces (Edwardsville IL, 2002), pp. 195-200, Contemp. Math. 328, Amer. Math. Soc, Providence, RI, 2003. http://dx.doi.org/10.1090/conm/328/05781.Google Scholar
[10] Haralampidou, M., Palacios, L., and Signoret, C., Multipliers inperfect locally m-convex algebras. Banach J. Math. Anal. 9 (2015), no. 1, 137–143. http://dx.doi.org/10.15352/bjma/09-1-11.Google Scholar
[11] Hogbe-Nlend, H., Les fondements de la theorie spectrale des algebres bornologiques. Bol. Soc. Brasil Mat. 3 (1972), 19–56. http://dx.doi.org/10.1007/BF02584840.Google Scholar
[12] Inoue, A., Locally C*-algebras. Mem. Faculty Sei. Kyushu Univ. SerA 25 (1971), 197–235. http://dx.doi.Org/1O.22O6/kyushumfs.25.1 97.Google Scholar
[13] Mallios, A., Topological algebras. Selected topics. North-Holland Mathematics Studies, 124. North-Holland, Amsterdam, 1986.Google Scholar
[14] Oudadess, M., Theoreme du type Gelfand-Naimark dans les algebres uniformement A-convexes. Ann. Sc. Math. Quebec, 9 (1985), 73–82.Google Scholar
[15] Oudadess, M., Une norme d'algebre de Banach dans les algebres uniformement A-convexes. Africa Math. 9 (1987), 15–22.Google Scholar
[16] Oudadess, M., Bounded struetures in locally A-convex algebras. Math. Stud. (Tartu), 4. Est. Math. Soc, Tartu, 2008, pp. 80-88.Google Scholar
[17] Oudadess, M., C*-bornological algebras. African Diaspora J. Math. 9 (2010), 87–95.Google Scholar
[18] Oudadess, M., Subnormable A-convex algebras. De Gruyter Proceedings in Mathematics (to appear).Google Scholar
[19] Phillips, N. C., Inverse limits of C*-algebras. J. Operator Tneory 19 (1988), 159–195.Google Scholar
[20] Rickart, C. E., General theory of Banach algebras. D. Van Nostrand, Princeton, N.J., 1960.Google Scholar
[21] Rudin, W., Functional analysis. McGraw-Hill, New York, 1973.Google Scholar
[22] Varopoulos, N. Th., Sur lesformes positives d’ une algebre de Banach. C. R. Acad. Sei. Paris 258 (1964), 2465–2467.Google Scholar