Article contents
Cliquishness and Quasicontinuity of Two-Variable Maps
Published online by Cambridge University Press: 20 November 2018
Abstract
We study the existence of continuity points for mappings 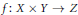 $f\,:\,X\,\times \,Y\,\to \,Z$ whose
$f\,:\,X\,\times \,Y\,\to \,Z$ whose  $x$ -sections
$x$ -sections 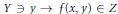 $Y\,\backepsilon\,y\,\to \,f\left( x,y \right)\,\in \,Z$ are fragmentable and
$Y\,\backepsilon\,y\,\to \,f\left( x,y \right)\,\in \,Z$ are fragmentable and 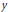 $y$ -sections
$y$ -sections  $X\,\backepsilon\,x\,\to \,f\left( x,y \right)\,\in \,Z$ are quasicontinuous, where
$X\,\backepsilon\,x\,\to \,f\left( x,y \right)\,\in \,Z$ are quasicontinuous, where 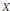 $X$ is a Baire space and
$X$ is a Baire space and 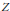 $Z$ is a metric space. For the factor
$Z$ is a metric space. For the factor 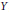 $Y$ , we consider two infinite “point-picking” games
$Y$ , we consider two infinite “point-picking” games 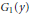 ${{G}_{1}}\,\left( y \right)$ and
${{G}_{1}}\,\left( y \right)$ and 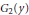 ${{G}_{2}}\,\left( y \right)$ defined respectively for each
${{G}_{2}}\,\left( y \right)$ defined respectively for each 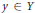 $y\,\in \,Y$ as follows: in the
$y\,\in \,Y$ as follows: in the  $n$ -th inning, Player I gives a dense set
$n$ -th inning, Player I gives a dense set 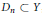 ${{D}_{n}}\,\subset \,Y$ , respectively, a dense open set
${{D}_{n}}\,\subset \,Y$ , respectively, a dense open set 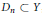 ${{D}_{n}}\,\subset \,Y$ . Then Player II picks a point
${{D}_{n}}\,\subset \,Y$ . Then Player II picks a point 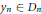 ${{y}_{n}}\,\in \,{{D}_{n}}$ ; II wins if
${{y}_{n}}\,\in \,{{D}_{n}}$ ; II wins if 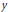 $y$ is in the closure of
$y$ is in the closure of 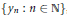 $\left\{ {{y}_{n}}\,:\,n\,\in \,\mathbb{N} \right\}$ , otherwise I wins. It is shown that (i)
$\left\{ {{y}_{n}}\,:\,n\,\in \,\mathbb{N} \right\}$ , otherwise I wins. It is shown that (i) 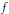 $f$ is cliquish if II has a winning strategy in
$f$ is cliquish if II has a winning strategy in 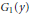 ${{G}_{1}}\,\left( y \right)$ for every
${{G}_{1}}\,\left( y \right)$ for every 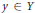 $y\,\in \,Y$ , and (ii)
$y\,\in \,Y$ , and (ii) 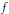 $f$ is quasicontinuous if the
$f$ is quasicontinuous if the  $x$ -sections of
$x$ -sections of 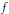 $f$ are continuous and the set of
$f$ are continuous and the set of 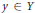 $y\,\in \,Y$ such that II has a winning strategy in
$y\,\in \,Y$ such that II has a winning strategy in 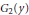 ${{G}_{2}}\,\left( y \right)$ is dense in
${{G}_{2}}\,\left( y \right)$ is dense in 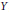 $Y$ . Item (i) extends substantially a result of Debs and item (ii) indicates that the problem of Talagrand on separately continuous maps has a positive answer for a wide class of “small” compact spaces.
$Y$ . Item (i) extends substantially a result of Debs and item (ii) indicates that the problem of Talagrand on separately continuous maps has a positive answer for a wide class of “small” compact spaces.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2013
References
- 2
- Cited by

