Article contents
Criteria for Commutativity in Large Groups
Published online by Cambridge University Press: 20 November 2018
Abstract
In this paper we prove the following:
-
1. Let
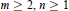 $m\ge 2,\,n\ge 1$ be integers and let
$m\ge 2,\,n\ge 1$ be integers and let 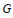 $G$ be a group such that
$G$ be a group such that 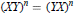 ${{(XY)}^{n}}\,=\,{{(YX)}^{n}}$ for all subsets
${{(XY)}^{n}}\,=\,{{(YX)}^{n}}$ for all subsets  $X,Y$ of size
$X,Y$ of size 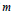 $m$ in
$m$ in 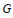 $G$ . Then
$G$ . Then-
a)
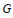 $G$ is abelian or a
$G$ is abelian or a  $\text{BFC}$ -group of finite exponent bounded by a function of
$\text{BFC}$ -group of finite exponent bounded by a function of 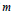 $m$ and
$m$ and 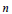 $n$ .
$n$ . -
b) If
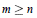 $m\ge n$ then
$m\ge n$ then 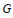 $G$ is abelian or
$G$ is abelian or 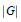 $|G|$ is bounded by a function of
$|G|$ is bounded by a function of 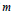 $m$ and
$m$ and 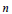 $n$ .
$n$ .
-
-
2. The only non-abelian group
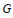 $G$ such that
$G$ such that 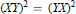 ${{(XY)}^{2}}\,=\,{{(YX)}^{2}}$ for all subsets
${{(XY)}^{2}}\,=\,{{(YX)}^{2}}$ for all subsets  $X,Y$ of size 2 in
$X,Y$ of size 2 in 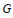 $G$ is the quaternion group of order 8.
$G$ is the quaternion group of order 8. -
3. Let
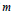 $m$ ,
$m$ , 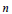 $n$ be positive integers and
$n$ be positive integers and 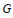 $G$ a group such that
$G$ a group such that 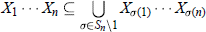 $${{X}_{1}}\cdot \cdot \cdot \,{{X}_{n}}\,\subseteq \,\bigcup\limits_{\sigma \in {{S}_{n}}\,\backslash \,1}{{{X}_{\sigma (1)}}\cdot \cdot \cdot \,{{X}_{\sigma (n)}}}$$
$${{X}_{1}}\cdot \cdot \cdot \,{{X}_{n}}\,\subseteq \,\bigcup\limits_{\sigma \in {{S}_{n}}\,\backslash \,1}{{{X}_{\sigma (1)}}\cdot \cdot \cdot \,{{X}_{\sigma (n)}}}$$
for all subsets 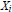 ${{X}_{i}}$ of size
${{X}_{i}}$ of size 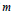 $m$ in
$m$ in 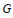 $G$ . Then
$G$ . Then 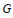 $G$ is
$G$ is 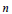 $n$ -permutable or
$n$ -permutable or 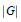 $|G|$ is bounded by a function of
$|G|$ is bounded by a function of 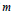 $m$ and
$m$ and 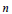 $n$ .
$n$ .
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1998
References
- 3
- Cited by

