Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-24T08:38:39.078Z Has data issue: false hasContentIssue false
  • English
  • Français

Enlarged Inclusion of Subdifferentials

Published online by Cambridge University Press:  20 November 2018

Lionel Thibault  and
Dariusz Zagrodny
Lionel Thibault
Affiliation:
Department of Mathematics, University Montpellier II, 34095 Montpellier, France
Dariusz Zagrodny
Affiliation:
Faculty of Mathemtics, and Natural Sciences, College of Sciences, Cardinal Stefan Wyszynski University, Warszawa 01-815, Poland
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

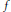This paper studies the integration of inclusion of subdifferentials. Under various verifiable conditions, we obtain that if two proper lower semicontinuous functions $f$ and $g$ have the subdifferential of 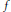$f$ included in the $\gamma $-enlargement of the subdifferential of $g$, then the difference of those functions is $\gamma $-Lipschitz over their effective domain.

Keywords

49J5246N1058C20subdifferentialdirectionally regular functionapproximate convex functionsubdifferentially and directionally stable function
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 48 , Issue 2 , 01 June 2005 , pp. 283 - 301
Copyright
Copyright © Canadian Mathematical Society 2005

References

[1] Borwein, J. M., Minimal CUSCOS and subgradients of Lipschitz functions. In: Fixed Point Theory and Applications, (Baillon, J. B. and Thera, M., eds.), Pitman Lectures Notes in Mathematics 252, Longman, Harlow, 1991, pp. 57–82.Google Scholar
[2] Clarke, F. H., Optimization and Nonsmooth Analysis. Wiley, New York, 1983.Google Scholar
[3] Correa, R. and Jofré, A., Tangentially continuous directional derivatives in nonsmooth analysis. J. Optim. Theory Appl. 61(1989), 1–21.Google Scholar
[4] Correa, R. and Thibault, L., Subdifferential analysis of bivariate separate regular functions. J. Math. Anal. Appl. 148(1990), 157–174.Google Scholar
[5] Gajek, L. and Zagrodny, D., Geometric mean value theorems for the Dini derivative. J. Math. Anal. Appl. 191(1995), 56–76.Google Scholar
[6] Geoffroy, M., Jules, F. and Lassonde, M., Integration of subdifferentials of lower semicontinuous functions. Preprint 00-02 (2000), Dept. Math. Université des Antilles et de la Guyane.Google Scholar
[7] Jourani, A., Subdifferentiability and subdifferential monotonicity of γ-paraconvex functions. Control Cybernet. 25(1996), 721–737.Google Scholar
[8] Ivanov, M. and Zlateva, N., Abstract subdifferential calculus and semi-convex functions. Serdica Math. J. 23(1997), 35–58.Google Scholar
[9] Mordukhovich, B. and Shao, Y., Nonsmooth sequential analysis in Asplund spaces. Trans. Amer. Math. Soc. 348(1996), 1235–1280.Google Scholar
[10] Ngai, H., Luc, D. T. and Théra, M., Approximate convex functions. J. Nonlinear Convex Anal. 1(2000), 155–176.Google Scholar
[11] Poliquin, R. A., Subgradient monotonicity and convex functions. Nonlinear Anal. 14(1990), 305–317.Google Scholar
[12] Poliquin, R. A., Integration of subdifferentials of nonconvex functions. Nonlinear Anal. 17(1991), 385–398.Google Scholar
[13] Rockafellar, R. T., Characterization of the subdifferentials of convex functions. Pacific J. Math. 17(1966), 497–510.Google Scholar
[14] Rockafellar, R. T., On the maximal monotonicity of subdifferential mappings. Pacific J. Math. 33(1970), 209–216.Google Scholar
[15] Rockafellar, R. T., Favorable classes of Lipschtz-continuous functions in subgradient optimization. In: Progress in Nondifferentiable Optimization, (Nurminski, E., ed.), IIASA Collaborative Proceedings Series, International Institute of Applied Systems Analysis, Laxenburg, Austria, 1982, pp. 125–143.Google Scholar
[16] Rolewicz, S., On the coincidence of some subdifferentials in the class of α(*)-paraconvex functions. Optimization 50(2001), 353–363.Google Scholar
[17] Spingarn, J. E., Submonotone subdifferentials of Lipschitz functions. Trans. Amer. Math. Soc. 264(1981), 77–89.Google Scholar
[18] Thibault, L., A note on the Zagrodny mean value theorem. Optimization 35(1995), 127–130.Google Scholar
[19] Thibault, L. and Zagrodny, D., Integration of subdifferentials of lower semicontinuous functions on Banach spaces. J. Math. Anal. Appl. 189(1995), 33–58.Google Scholar
[20] Zagrodny, D., Approximate mean value theorem for upper subderivatives. Nonlinear Anal. 12(1988), 1413–1428.Google Scholar