No CrossRef data available.
Article contents
Equivalent Definitions of Infinite Positive Elements in Simple C*-algebras
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
We prove the equivalence of three definitions given by different comparison relations for infiniteness of positive elements in simple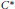 
${{C}^{*}}$-algebras.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2010
References
[1] Blackadar, B., K-theory for operator algebras. Mathematical Sciences Research Institute Publications, 5, Springer-Verlag, New York, 1986.Google Scholar
[2] Blackadar, B. and Cuntz, J., The structure of stable algebraically simple C*-algebras. Amer. J. Math.
104(1982), no. 4, 813–822. doi:10.2307/2374206Google Scholar
[3] Cuntz, J., Simple C*-algebras generated by isometries. Comm. Math. Phys.
57(1977), no. 2, 173–185. doi:10.1007/BF01625776Google Scholar
[4] Cuntz, J., The structure of multiplication and addition in simple C*-algebras. Math. Scand.
40(1977), no. 2, 215–233.Google Scholar
[5] Cuntz, J., Dimension functions on simple C*-algebras. Math. Ann.
233(1978), no. 2, 145–153. doi:10.1007/BF01421922Google Scholar
[6] Cuntz, J., K-theory for certain C*-algebras. Ann. of Math.
113(1981), no. 1, 181–197. doi:10.2307/1971137Google Scholar
[7] Elliott, G. A. and Fang, X., Simple inductive limits of C*-algebras with building blocks from spheres of odd dimension. In: Operator algebra and operator theory, Contemp. Math., 228, American Mathematical Society, Providence, RI, 1998, pp. 79–86.Google Scholar
[8] Fang, X., The invariant continuous-trace C*-algebras by the actions of compact abelian groups. Chinese Ann. of Math.(B)
19(1998), no. 4, 489–498.Google Scholar
[9] Fang, X., The simplicity and real rank zero property of the inductive limit of continuous trace C*-algebras. Analysis
19(1999), no. 4, 377–389.Google Scholar
[10] Fang, X., Graph C*-algebras and their ideals defined by Cuntz–Krieger family of possibly row-infinite directed graphs. Integral Equations Operator Theory
54(2006), no. 3, 301–316. doi:10.1007/s00020-004-1363-zGoogle Scholar
[11] Fang, X., The real rank zero property of crossed product. Proc. Amer. Math. Soc.
134(2006), no. 10, 3015–3024. doi:10.1090/S0002-9939-06-08357-2Google Scholar
[12] Kirchberg, E. and Rørdam, M., Infinite non-simple C*-algebras: absorbing the Cuntz algebra 
. Adv. Math.
167(2002), no. 2, 195–264. doi:10.1006/aima.2001.2041Google Scholar
. Adv. Math.
167(2002), no. 2, 195–264. doi:10.1006/aima.2001.2041Google Scholar[13] Lin, H., An introduction to the classification of amenable C*-algebras.
World Scientific Publishing Co., Inc., River Edge, NJ, 2001.Google Scholar
[14] Lin, H., Classification of simple C*-algebras and higher dimensional noncommutative tori. Ann. of Math.
157(2003), no. 2, 521–544. doi:10.4007/annals.2003.157.521Google Scholar
[15] Lin, H. and Zhang, S., On infinite simple C*-algebras. J. Funct. Anal.
100(1991), no. 1, 221–231. doi:10.1016/0022-1236(91)90109-IGoogle Scholar
[16] Pedersen, G. K., C*-algebras and their automorphism groups. London Mathematical Society Monographs, 14, Academic Press, London–New York, 1979.Google Scholar
[17] Rørdam, M., Ideals in the multiplier algebra of a stable C*-algebra. J. Operator Theory
25(1991), no. 2, 283–298.Google Scholar
[18] Rørdam, M., On the structure of simple C*-algebras tensored with a UHF-algebra. II. J. Funct. Anal.
107(1992), no. 2, 255–269. doi:10.1016/0022-1236(92)90106-SGoogle Scholar
[19] Rørdam, M., A simple C*-algebra with a finite and an infinite projection. Acta Math.
191(2003), no. 1, 109–142. doi:10.1007/BF02392697Google Scholar
[20] Toms, A. S., On the classification problem for nuclear C*-algebras. Ann. of Math.
167(2008), no. 3, 1029–1044. doi:10.4007/annals.2008.167.1029Google Scholar
You have
Access