Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-24T17:55:42.054Z Has data issue: false hasContentIssue false
  • English
  • Français

Extension of the Riemann ξ-Function's Logarithmic Derivative Positivity Region to Near the Critical Strip

Published online by Cambridge University Press:  20 November 2018

Kevin A. Broughan
Kevin A. Broughan*
Affiliation:
Department of Mathematics, University of Waikato, Hamilton, New Zealand e-mail: kab@waikato.ac.nz
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If 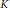$K$ is a number field with 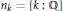${{n}_{k}}\,=\,\left[ k\,:\,\mathbb{Q} \right]$, and 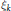${{\xi }_{k}}$ the symmetrized Dedekind zeta function of the field, the inequality

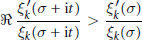$$\Re \frac{\xi _{k}^{'}\left( \sigma \,+\,\text{i}t \right)}{{{\xi }_{k}}\left( \sigma \,+\,\text{i}t \right)}\,>\,\frac{\xi _{k}^{'}\left( \sigma \right)}{{{\xi }_{k}}\left( \sigma \right)}$$

for 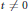$t\,\ne \,0$ is shown to be true for 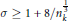$\sigma \,\ge \,1\,+\,8/n_{k}^{\frac{1}{3}}$ improving the result of Lagarias where the constant in the inequality was 9. In the case 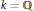$k\,=\,\mathbb{Q}$ the inequality is extended to 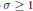$\sigma \,\ge \,1$ for all $t$ sufficiently large or small and to the region 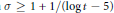$\sigma \,\ge \,1\,+\,1/\left( \log \,t\,-\,5 \right)$ for all 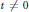$t\,\ne \,0$. This answers positively a question posed by Lagarias.

Keywords

11M2611R42Riemann zeta functionxi functionzeta zeros
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 52 , Issue 2 , 01 June 2009 , pp. 186 - 194
Copyright
Copyright © Canadian Mathematical Society 2009

References

[1] Alzer, H., On some inequalities for the gamma and psi functions. Math. Comp. 66(1997), no. 217, 373–389.Google Scholar
[2] Alzer, H., Sharp inequalities for the digamma and polygamma functions. Forum. Math. 16(2004), no. 2, 181–221.Google Scholar
[3] Cheng, Y., An explicit upper bound for the Riemann zeta-function near the line σ = 1 . Rocky Mountain J. Math. 29(1999), no. 1, 115–140.Google Scholar
[4] Delange, H., Une remarque sur la dérivée logarithmique de la fonction zêta de Riemann. Colloq. Math. 53(1987), no. 2, 333–335.Google Scholar
[5] Garunkstis, R., On a positivity property of the Riemann ζ-function. Liet. Mat. Rink 42(2002), no. 2, 179–184.Google Scholar
[6] Hinkkanen, A., On functions of bounded type. Complex Variables Theory Appl. 34(1997), no. 1–2, 119–139.Google Scholar
[7] Ivić, A., The Riemann zeta-function. Theory and Applications. Wiley, New York, 1985.Google Scholar
[8] Lagarias, J. C., On a positivity property of the Riemann ζ-function. Acta Arith. 89(1999), no. 3, 217–234.Google Scholar
[9] Levinson, N. and Montgomery, H. L., Zeros of the derivatives of the Riemann zetafunction. Acta Math. 133(1974), 49–65.Google Scholar
[10] Richert, H.-E., Zur Awchätzung der Riemannschen Zetafunktion in der Nähe der Vertikalen σ = 1 . Math. Ann. 169(1967), 97–101.Google Scholar
[11] Titchmarsh, E. C., The theory of the Riemann Zeta-function. Second edition, Oxford University Press, New York, 1986.Google Scholar
[12] Wedeniwski, S., Results connected with the first 100 billion zeros of the Riemann function. http://www.zetagrid.net/zeta/math/zeta.result.100billion.zeros.html.Google Scholar