A theorem of Gekeler compares the number of non-isomorphic automorphic representations associated with the space of cusp forms of weight 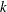$k$ on 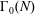$\unicode[STIX]{x0393}_{0}(N)$ to a simpler function of 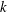$k$ and 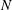$N$, showing that the two are equal whenever 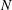$N$ is squarefree. We prove the converse of this theorem (with one small exception), thus providing a characterization of squarefree integers. We also establish a similar characterization of prime numbers in terms of the number of Hecke newforms of weight 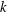$k$ on 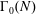$\unicode[STIX]{x0393}_{0}(N)$.

It follows that a hypothetical fast algorithm for computing the number of such automorphic representations for even a single weight 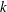$k$ would yield a fast test for whether 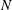$N$ is squarefree. We also show how to obtain bounds on the possible square divisors of a number 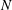$N$ that has been found not to be squarefree via this test, and we show how to probabilistically obtain the complete factorization of the squarefull part of 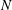$N$ from the number of such automorphic representations for two different weights. If in addition we have the number of such Hecke newforms for even a single weight 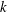$k$, then we show how to probabilistically factor 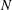$N$ entirely. All of these computations could be performed quickly in practice, given the number(s) of automorphic representations and modular forms as input.