Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kim, Tae-Hwa
1992.
Nonlinear ergodic theorems of almost-orbits of non-Lipschitzian semigroups.
Kodai Mathematical Journal,
Vol. 15,
Issue. 2,

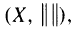 it is shown that if G is a commutative semigroup of continuous selfmappings on X which is proximately nonexpansive, then a common fixed point exists if there is an x
it is shown that if G is a commutative semigroup of continuous selfmappings on X which is proximately nonexpansive, then a common fixed point exists if there is an x