No CrossRef data available.
Article contents
Generating Some Symmetric Semi-classical Orthogonal Polynomials
Published online by Cambridge University Press: 20 November 2018
Abstract
We show that if  $v$ is a regular semi-classical form (linear functional), then the symmetric form
$v$ is a regular semi-classical form (linear functional), then the symmetric form  $u$ defined by the relation
$u$ defined by the relation 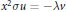 ${{x}^{2}}\sigma u\,=\,-\lambda v$ , where
${{x}^{2}}\sigma u\,=\,-\lambda v$ , where 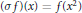 $\left( \sigma f \right)\left( x \right)\,=\,f\left( {{x}^{2}} \right)$ and the odd moments of
$\left( \sigma f \right)\left( x \right)\,=\,f\left( {{x}^{2}} \right)$ and the odd moments of  $u$ are 0, is also regular and semi-classical form for every complex
$u$ are 0, is also regular and semi-classical form for every complex  $\lambda $ except for a discrete set of numbers depending on
$\lambda $ except for a discrete set of numbers depending on  $v$ . We give explicitly the three-term recurrence relation and the structure relation coefficients of the orthogonal polynomials sequence associated with
$v$ . We give explicitly the three-term recurrence relation and the structure relation coefficients of the orthogonal polynomials sequence associated with  $u$ and the class of the form
$u$ and the class of the form  $u$ knowing that of
$u$ knowing that of  $v$ . Weconclude with an illustrative example.
$v$ . Weconclude with an illustrative example.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2015

