Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T05:04:00.188Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear Conjugacy

Part of: Semigroups

Published online by Cambridge University Press:  29 January 2019

Benjamin Steinberg
Benjamin Steinberg*
Affiliation:
Department of Mathematics, City College of New York, Convent Avenue at 138th Street, New York, New York 10031, USA Email: bsteinberg@ccny.cuny.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We say that two elements of a group or semigroup are 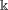$\Bbbk$-linear conjugates if their images under any linear representation over 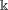$\Bbbk$ are conjugate matrices. In this paper we characterize 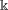$\Bbbk$-linear conjugacy for finite semigroups (and, in particular, for finite groups) over an arbitrary field 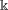$\Bbbk$.

Keywords

monoidrepresentation theoryconjugacy

MSC classification

Primary: 20M30: Representation of semigroups; actions of semigroups on sets
Type
Article
Information
Canadian Mathematical Bulletin , Volume 62 , Issue 4 , December 2019 , pp. 886 - 895
Copyright
© Canadian Mathematical Society 2019 

Footnotes

This work was partially supported by grants from the Simons Foundation (#245268), the Binational Science Foundation of Israel and the U.S.A. (#2012080) by a CUNY Collaborative Incentive Research Grant, by NSA MSP #H98230-16-1-0047 and by a Fulbright Scholar award.

References

Berman, S. D., The number of irreducible representations of a finite group over an arbitrary field . Dokl. Akad. Nauk SSSR (N.S.) 106(1956), 767–769.Google Scholar
Clifford, A. H. and Preston, G. B., The algebraic theory of semigroups. I . Mathematical Surveys, 7. American Mathematical Society, Providence, RI, 1961.Google Scholar
Kovács, L. G., The permutation lemma of Richard Brauer . Bull. Lond. Math. Soc. 14(1982), no. 2, 127–128. https://doi.org/10.1112/blms/14.2.127 Google Scholar
Kovács, L. G., Semigroup algebras of the full matrix semigroup over a finite field . Proc. Amer. Math. Soc. 116(1992), no. 4, 911–919. https://doi.org/10.2307/2159467 Google Scholar
Masuda, A. M., Quoos, L., and Steinberg, B., Character theory of monoids over an arbitrary field . J. Algebra 431(2015), 107–126. https://doi.org/10.1016/j.jalgebra.2015.02.017 Google Scholar
McAlister, D. B., Characters of finite semigroups . J. Algebra 22(1972), 183–200. https://doi.org/10.1016/0021-8693(72)90111-1 Google Scholar
Propp, J., Distinguishing combinatorial maps by their linearizations. http://mathoverflow.net/q/198144 (version: 2015-02-22).Google Scholar
Rhodes, J. and Steinberg, B., The q-theory of finite semigroups . Springer Monographs in Mathematics. Springer, New York, 2009. https://doi.org/10.1007/b104443 Google Scholar
Rhodes, J. and Zalcstein, Y., Elementary representation and character theory of finite semigroups and its application . In: Monoids and semigroups with applications . World Sci. Publ., River Edge, NJ, 1991, pp. 334–367.Google Scholar
Solomon, L., Representations of the rook monoid . J. Algebra 256(2002), no. 2, 309–342. https://doi.org/10.1016/S0021-8693(02)00004-2 Google Scholar
Steinberg, B., Representation theory of finite monoids . Universitext. Springer, Cham, 2016. https://doi.org/10.1007/978-3-319-43932-7 Google Scholar