Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Janos, Ludvik
2001.
Categorical Perspectives.
p.
197.

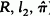 ) on the Hilbert space l
) on the Hilbert space l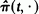 are linear operators on l
are linear operators on l