No CrossRef data available.
Article contents
On Classes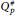 
for Hyperbolic Riemann Surfaces
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
The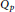 
${{Q}_{p}}$ spaces of holomorphic functions on the disk, hyperbolic Riemann surfaces or complex unit ball have been studied deeply. Meanwhile, there are a lot of papers devoted to the 
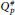$Q_{p}^{\#}$ classes of meromorphic functions on the disk or hyperbolic Riemann surfaces. In this paper, we prove the nesting property (inclusion relations) of 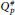$Q_{p}^{\#}$ classes on hyperbolic Riemann surfaces. The same property for 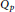${{Q}_{p}}$ spaces was also established systematically and precisely in earlier work by the authors of this paper.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2016
References
[1]
Ahlfors, L., Conformai invariants, topics in geometric function theory. McGraw-Hill Series in Higher Mathematics, Mcgraw-Hill, New York, 1973.Google Scholar
[2]
Anderson, J. M., Clunie, J., and Pommerenke, Ch., On Block functions and normal functions.
J. Reine Angew. Math.
240(1974), 12–37.Google Scholar
[3]
Aulaskari, R., On V MO A for Riemann surfaces.
Canad. J. Math.
40(1988), no. 5,1174-1185. http://dx.doi.Org/10.4153/CJM-1988-049-9
Google Scholar
[4]
Aulaskari, R. and Chen, H., Area inequality and Qp norm.
J. Funct. Anal.
221(2005), no. 1,1-24. http://dx.doi.Org/10.1016/j.jfa.2004.12.007
Google Scholar
[5]
Aulaskari, R., He, Y., Ristioja, J., and Zhao, R., Qp spaces on Riemann surfaces.
Canad. J. Math.
50(1998), no. 3, 449–464. http://dx.doi.Org/10.4153/CJM-1998-024-4
Google Scholar
[6]
Aulaskari, R. and Lappan, P., Criteria for an analytic function to be Block and a harmonic or meromorphic function to be normal. In: Complex analysis and its applications (Hong Kong, 1993), Pitman Res. Notes Math. Ser., 305, Longman Sci. Tech., Harlow, 1994, pp. 136–146.Google Scholar
[7]
Aulaskari, R., Xiao, J., and Zhao, R., On subspaces and subsets ofBMOA and UBC.
Analysis
15(1995), no. 2, 101–121.Google Scholar
[8]
Dufresnoy, J., Sur l'aire sphérique décrite par les valeurs d'une fonction mefomorphe.
Bull. Sci. Math.
65(1941), 214–219.Google Scholar
[9]
Kobayashi, S., Image areas and BMO norms of analytic functions.
Kodai Math. J.
8(1985), no. 2, 163–170. http://dx.doi.Org/10.2996/kmj71138037045
Google Scholar
[10]
Kobayashi, S., Range sets and BMO norms of analytic functions.
Canad. J. Math.
36(1984), no. 4, 747–755. http://dx.doi.Org/10.4153/CJM-1984-042-6
Google Scholar
[11]
Lehto, O. and Virtanen, K. I., Boundary behaviour and normal meromorphic functions.
Acta Math.
97(1957), 47–65. http://dx.doi.Org/10.1007/BF02392392
Google Scholar
[12]
Ouyang, C., Yang, W., and Zhao, R., Mb'bius invariant Qp spaces associated with the Green's function on the unit ball o/C”. Pacific J. Math.
182(1998), no. 1, 69–99. http://dx.doi.Org/10.2140/pjm.1998.182.69
Google Scholar
[13]
Xiao, J., Carleson measure, atomic decomposition and free interpolation from Bloch space.
Ann. Acad. Sci. Fenn. Ser. AI Math.
19(1994), no. 1, 35–46.Google Scholar
[14]
Xiao, J., Holomorphic Q classes. Lecture Notes in Mathematics, 1767, Springer-Verlag, Berlin, 2001.Google Scholar
[15]
Yamashita, S., Functions of uniformly bounded characteristic.
Ann. Acad. Sci. Fenn. Ser. A I Math.
7(1982), no. 2, 349–367. http://dx.doi.Org/10.5186/aasfm.1982.0733
Google Scholar
[16]
Yamashita, S., Some unsolved problems on meromorphic functions of uniformly bounded characteristic.
Internat. J. Math. Math. Sci.
8(1985), no. 3, 477–482. http://dx.doi.Org/!0.1155/SO161171285000527
Google Scholar
You have
Access