No CrossRef data available.
Article contents
On Deformations of the Complex Structure on the Moduli Space of Spatial Polygons
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
For an integer 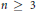 $n\,\ge \,3$ , let
$n\,\ge \,3$ , let 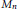 ${{M}_{n}}$ be the moduli space of spatial polygons with
${{M}_{n}}$ be the moduli space of spatial polygons with  $n$ edges. We consider the case of odd
$n$ edges. We consider the case of odd  $n$ . Then
$n$ . Then 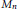 ${{M}_{n}}$ is a Fano manifold of complex dimension
${{M}_{n}}$ is a Fano manifold of complex dimension 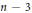 $n\,-\,3$ . Let
$n\,-\,3$ . Let 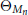 ${{\Theta }_{{{M}_{n}}}}$ be the sheaf of germs of holomorphic sections of the tangent bundle
${{\Theta }_{{{M}_{n}}}}$ be the sheaf of germs of holomorphic sections of the tangent bundle 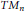 $T{{M}_{n}}$ . In this paper, we prove
$T{{M}_{n}}$ . In this paper, we prove 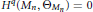 ${{H}^{q}}\left( {{M}_{n}},\,{{\Theta }_{{{M}_{n}}}} \right)\,=\,0$ for all
${{H}^{q}}\left( {{M}_{n}},\,{{\Theta }_{{{M}_{n}}}} \right)\,=\,0$ for all 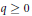 $q\,\ge \,0$ and all odd
$q\,\ge \,0$ and all odd  $n$ . In particular, we see that the moduli space of deformations of the complex structure on
$n$ . In particular, we see that the moduli space of deformations of the complex structure on 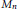 ${{M}_{n}}$ consists of a point. Thus the complex structure on
${{M}_{n}}$ consists of a point. Thus the complex structure on 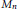 ${{M}_{n}}$ is locally rigid.
${{M}_{n}}$ is locally rigid.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2002
References
[1]
Brion, M., Cohomologie équivariante des points semi-stables. J. Reine Angew.Math. 421 (1991), 421–1991.Google Scholar
[2]
Griffiths, P. and Harris, J., Principles of algebraic geometry. Wiley-Interscience, New York, 1978.Google Scholar
[3]
Hausmann, J.-C. and Knutson, A., The cohomology ring of polygon spaces. Ann. Inst. Fourier (Grenoble) 48 (1998), 48–1998.Google Scholar
[4]
Kamiyama, Y. and Tezuka, M., Symplectic volume of the moduli space of spatial polygons. J. Math. Kyoto Univ. 39 (1999), 39–1999.Google Scholar
[5]
Kapovich, M. and Millson, J., The symplectic geometry of polygons in Euclidean space. J. Differential Geom. 44 (1996), 44–1996.Google Scholar
[6]
Kirwan, F., Cohomology of quotients in symplectic and algebraic geometry. Mathematical Notes 31, Princeton University Press, Princeton, 1984.Google Scholar
[7]
Kirwan, F., The cohomology rings of moduli spaces of bundles over Riemann surfaces. J. Amer. Math. Soc. 5 (1992), 5–1992.Google Scholar
[8]
Klyachko, A., Spatial polygons and stable configurations of points in the projective line. In: Algebraic geometry and its applications, Yaroslavl', 1992, 67–84, Aspects Math. E25, Vieweg, Braunschweig, 1994.Google Scholar
[9]
Kodaira, K., Complex manifolds and deformation of complex structures. Grundlehren der Mathematischen Wissenschaften 283, Springer-Verlag, 1986.Google Scholar
[10]
Siu, Y.-T. and Trautmann, G., Gap-sheaves and extension of coherent analytic subsheaves. Lecture Notes in Mathematics 172, Springer-Verlag, 1971.Google Scholar

