Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-22T05:37:36.407Z Has data issue: false hasContentIssue false
  • English
  • Français

On framings of links in 3-manifolds

Part of: Low-dimensional topology

Published online by Cambridge University Press:  21 September 2020

Rhea Palak Bakshi ,
Dionne Ibarra ,
Gabriel Montoya-Vega ,
Józef H. Przytycki  and
Deborah Weeks
Rhea Palak Bakshi
Affiliation:
Department of Mathematics, The George Washington University, Washington DC, USAe-mail:rhea_palak@gwu.edudfkunkel@gwu.edugmontoyavega@gwu.edudeweeks@gwu.edu
Dionne Ibarra
Affiliation:
Department of Mathematics, The George Washington University, Washington DC, USAe-mail:rhea_palak@gwu.edudfkunkel@gwu.edugmontoyavega@gwu.edudeweeks@gwu.edu
Gabriel Montoya-Vega
Affiliation:
Department of Mathematics, The George Washington University, Washington DC, USAe-mail:rhea_palak@gwu.edudfkunkel@gwu.edugmontoyavega@gwu.edudeweeks@gwu.edu
Józef H. Przytycki*
Affiliation:
Department of Mathematics, The George Washington University, Washington DC, USA and Department of Mathematics, University of Gdańsk, Gdańsk, Poland
Deborah Weeks
Affiliation:
Department of Mathematics, The George Washington University, Washington DC, USAe-mail:rhea_palak@gwu.edudfkunkel@gwu.edugmontoyavega@gwu.edudeweeks@gwu.edu
*
e-mail:przytyck@gwu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

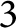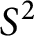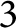We show that the only way of changing the framing of a link by ambient isotopy in an oriented $3$ -manifold is when the manifold has a properly embedded non-separating $S^{2}$ . This change of framing is given by the Dirac trick, also known as the light bulb trick. The main tool we use is based on McCullough’s work on the mapping class groups of $3$ -manifolds. We also relate our results to the theory of skein modules.

Keywords

Knotslinks3-manifoldsframings of linksskein modulesspin structuresDehn homeomorphismsincompressible surfaces

MSC classification

Primary: 57M27: Invariants of knots and 3-manifolds
Secondary: 57M25: Knots and links in $S^3$
Type
Article
Information
Canadian Mathematical Bulletin , Volume 64 , Issue 4 , December 2021 , pp. 752 - 764
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The fourth author was partially supported by Simons Collaboration Grant-637794 and the CCAS Dean’s Research Chair award.

References

Barrett, J. W., Skein spaces and spin structures . Math. Proc. Camb. Philos. Soc. 126(1999), no. 2, 267–275. http://dx.doi.org/10.1017/S03004198003168 CrossRefGoogle Scholar
Cahn, P., Chernov, V., and Sadykov, R., The number of framings of a knot in a 3-manifold . J. Knot Theory Ramif. 23(2014), no. 13, 1450072, 9 pp. http://dx.doi.org/10.1142/S0218216514500722 CrossRefGoogle Scholar
Chernov, V., Framed knots in 3-manifolds and affine self-linking numbers . J. Knot Theory Ramif. 14(2005), no. 6, 791–818. http://dx.doi.org/10.1142/S0218216505004056 CrossRefGoogle Scholar
Das, S., Francis, G., Hart, J., Hartman, C., Heyn-Cubacub, J., Kauffman, L. H., Plepys, D., and Sandin, D. J., Air on the Dirac strings. https://www.youtube.com/watch?v=CYBqIRM8GiY Google Scholar
Gabai, D., Meyerhoff, G. R., and Thurston, N., Homotopy hyperbolic 3-manifolds are hyperbolic . Ann. of Math. 157(2003), no. 2, 335–431. http://dx.doi.org/10.4007/annals.2003.157.335 CrossRefGoogle Scholar
Gunningham, S., Jordan, D., Safronov, P., The finiteness conjecture for skein modules. Preprint, 2020. arXiv:1908.05233 Google Scholar
Hong, S. and McCullough, D., Mapping class groups of $3$ -manifolds, then and now. In: Geometry and topology down under, Contemp. Math., 597, Amer. Math. Soc., Providence, RI, 2013, pp. 53–63. http://dx.doi.org/10.1090/conm/597/11768 CrossRefGoogle Scholar
Hoste, J. and Przytycki, J. H., Homotopy skein modules of orientable $3$ -manifolds . Math. Proc. Camb. Philos. Soc. 108(1990), no. 3, 475–488. http://dx.doi.org/10.1017/S0305004100069371 CrossRefGoogle Scholar
Hudson, J. F. P., Piecewise linear topology . University of Chicago Lecture Notes prepared with the assistance of J. L. Shaneson and J. Lees, W. A. Benjamin, Inc., New York-Amsterdam, 1969.Google Scholar
Kirby, R., Problems in low dimensional manifold theory. In: Algebraic and geometric topology (Proc. Sympos. Pure Math., Stanford Univ., Stanford, CA, 1976), Part 2, Proc. Sympos. Pure Math., XXXII, Amer. Math. Soc., Providence, RI, 1978, pp. 273–312.Google Scholar
McCullough, D., Mappings of reducible 3-manifolds . In: Geometric and algebraic topology, Banach Center Publ., 18, PWN, Warsaw, 1986, pp. 61–76.Google Scholar
McCullough, D., Homeomorphisms which are Dehn twists on the boundary . Algebr. Geom. Topol. 6(2006), 1331–1340. http://dx.doi.org/10.2140/agt.2006.6.1331 CrossRefGoogle Scholar
McCullough, D. and Miller, A., Homeomorphisms of 3-manifolds with compressible boundary . Mem. Amer. Math. Soc. 61(1986), no. 344, 100 pp. http://dx.doi.org/10.1090/memo/0344 Google Scholar
Ohtsuki, T., Problems on invariants of knots and 3-manifolds. In: Invariants of knots in 3-manifolds (Kyoto, 2001), Geom. Topol. Monogr., 4, Geom. Topol. Publ. Coventry, 2002. http://dx.doi.org/10.2140/gtm.2002.4 CrossRefGoogle Scholar
Papakyriakopoulos, C. D., On Dehn’s lemma and the asphericity of knots . Ann. of Math. (2) 66(1957), 1–26. http://dx.doi.org/10.2307/1970113 CrossRefGoogle Scholar
Przytycki, J. H., Skein modules of 3-manifolds. Bull. Polish Acad. Sci. Math. 39(1991), no. 1–2, 91–100.Google Scholar
Przytycki, J. H., A $q$ -analogue of the first homology group of a $3$ -manifold. In: Perspectives on quantization (South Hadley, MA, 1996), Contemp. Math., 214, Amer. Math. Soc., Providence, RI, 1998, pp. 135–144. http://dx.doi.org/10.1090/conm/214/02910 Google Scholar
Przytycki, J. H., Skein modules (Chapter IX of “KNOTS: From combinatorics of knot diagrams to combinatorial topology based on knots”). Preprint, 2006. arXiv:math/0602264Google Scholar
Przytycki, J. H. and Sikora, A. S., On skein algebras and $\mathrm{SL}\left(2,\mathbb{C}\right)$ -character varieties. Topology 39(2000), no. 1, 115–148. http://dx.doi.org/10.1016/S0040-9383(98)00062-7 CrossRefGoogle Scholar
Stiefel, E., Richtungsfelder und Fernparallelismus in n-dimensionalen Mannigfaltigkeiten . (German) Comment. Math. Helv. 8(1935), no. 1, 305–353. http://dx.doi.org/10.1007/BF01199559 CrossRefGoogle Scholar
Turaev, V. G., Euler structures, nonsingular vector fields, and Reidemeister-type torsions [in Russian]. Izv. Akad. Nauk SSSR Ser. Mat. 53(1989), no. 3, 607–643, 672; translation in Math. USSR-Izv. 34(1990), no. 3, 627–662. http://dx.doi.org/10.1070/IM1990v34n03ABEH000676 Google Scholar
Waldhausen, F., Eine Klasse von 3-dimensionalen Mannigfaltigkeiten. I, II [in German]. Invent. Math. 3(1967), 308–333; ibid. 4(1967), 87–117. http://dx.doi.org/10.1007/BF01402956 CrossRefGoogle Scholar